hxy的博客

Mia san Mia!

0%

手写一个计算器

发表于 更新于 分类于 Valine：

在学习C语言的时候，曾经写过一个能实现四则运算的计算器大作业，当年觉得云里雾里，好难，其实搞懂了逆波兰表达式的原理和巧妙利用栈这个数据结构，就可以实现，但是其中要考虑一些细节，不手写一遍根本记不得。我现在最熟悉的语言自然是js，自然选择它重复当年的思路，力扣上只有逆波兰表达式求值和包括+-和括号的，因此选择了牛客上的表达式求值来做，当然js可以用eval函数一行搞定，不过这么做没什么意义，主要是为了复习计算机的基础知识，还是自己动手，丰衣足食。

题目描述

请写一个整数计算器，支持加减乘三种运算和括号。

示例1

输入

1
"1+2"

返回值

1
3

示例2

输入

1
"(2*(3-4))*5"

返回

1
-10

示例3

输入

1
"3+2*3*4-1"

返回值

1
26

实现逆波兰表达式

我选择将问题拆解成2步，完成这个问题，第一步是实现逆波兰表达式，消除所有括号。我们常用的计算表达式是中缀表达式，而逆波兰表达式是后缀表达式。

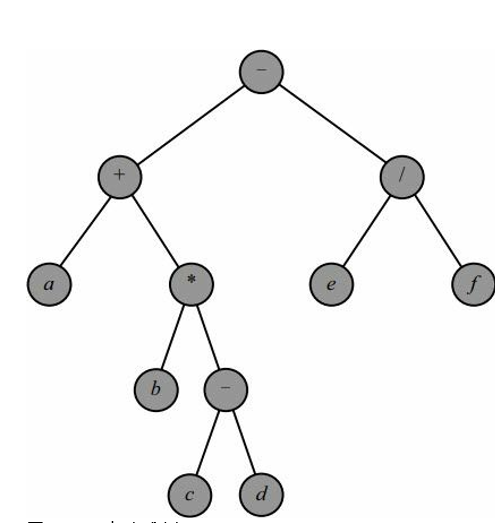
具体理解起来，将表达式写作二叉树的形式。例如，我们正常情况下看到的数学表达式a+b*(c-d)-e/f可以表示成如下所示的二叉树

对应于这棵二叉树是中序遍历，当然建立这棵树的过程需要考虑运算符的优先级，括号的配对，栈的使用。因此常规的表达式叫作中序表达式。而按照后序遍历的后序表达式就被称作逆波兰表达式，该表达式写作abcd-*+ef/-，这样可以很方便的进行计算。

将一个普通的中序表达式转换为逆波兰表达式的一般算法是：

1、首先构造一个运算符栈，此运算符在栈内遵循越往栈顶优先级越高的原则。（>*/>+-

2、读入一个中缀表达式，要注意末尾如果是数也要读入。

3、从左至右扫描该中缀表达式，如果当前字符是数字，则分析到该数字串的结束，并将该数字串保存至数组。

4、如果不是数字，该字符则是运算符，此时需比较该运算符与运算符栈顶运算符的优先关系：

（1）、若该运算符优先级高于栈顶运算符优先级别（或栈为空），则直接将该运算符压入运算符栈中；

（2）、若该运算符优先级小于或等于此运算符栈顶的运算符，则弹出栈顶运算符并保存至数组，重复比较、输出，直到栈为空或该运算符优先级高于栈顶运算符，然后将该运算符入栈。

5、重复上述操作(3)-(4)直至扫描完整个简单算术表达式，确定所有字符都得到正确处理，输出结果便是中缀表达式转化为逆波兰表示的简单算术表达式。

具体的实现方式，需要在原先的函数中设定两个栈和一个字符串，第一个栈用来保存逆波兰表达式序列（其实后来并没有利用栈的性质，只用了数组，如果一遍操作生成最终结果的话需要利用），第二个栈用来保存运算符，即运算符栈，字符串用来保存当前数

首先声明这些变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 * 返回表达式的值
 * @param s string字符串 待计算的表达式
 * @return int整型
 */
function solve( s ) {
    // write code here
    // 中缀转后缀
    let stack = [];
    let syStack = [];
    let num = "";
}
module.exports = {
    solve : solve
};

接下来遍历字符串，首先处理数字，使其能计算每个数的值，从这一步开始，仅保留主函数

1
2
3
4
5
6
7
8
9
10
function solve( s ) {
    let stack = [];
    let syStack = [];
    let num = "";
    for (let char of s) {
        if (char >= '0' && char <= '9') {
            num += char;
        }
    }
}

考虑符号的分类，其中括号>乘号>加减，其中括号要分成两类(和)，其中(必须入运算符栈，)必须找到对应的(并将两者之间的运算符全部出栈，注意处理符号的时候要将数保存进入第一个栈中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
function solve( s ) {
    // write code here
    // 中缀转后缀
    let stack = [];
    let syStack = [];
    let num = "";
    for (let char of s) {
        if (char >= '0' && char <= '9') {
            num += char;
        } else if (char === '(') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            syStack.push(char);
        } else if (char === '+' || char === '-') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] !== '(') {
                stack.push(syStack.pop());
            }
            syStack.push(char);
        } else if (char === '*') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] === '*') {
                stack.push(syStack.pop());
            }
            syStack.push(char);
        } else if (char === ')') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] !== '(') {
                stack.push(syStack.pop());
            }
            syStack.pop();
        }
    }
}

这里要注意最后一个如果是数需要再次保存，如果还有符号在运算符栈中需要出栈操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
function solve( s ) {
    // write code here
    // 中缀转后缀
    let stack = [];
    let syStack = [];
    let num = "";
    for (let char of s) {
        if (char >= '0' && char <= '9') {
            num += char;
        } else if (char === '(') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            syStack.push(char);
        } else if (char === '+' || char === '-') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] !== '(') {
                stack.push(syStack.pop());
            }
            syStack.push(char);
        } else if (char === '*') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] === '*') {
                stack.push(syStack.pop());
            }
            syStack.push(char);
        } else if (char === ')') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] !== '(') {
                stack.push(syStack.pop());
            }
            syStack.pop();
        }
    }
    if (num !== '') {
        stack.push(num);
    }
    while (syStack.length) {
        stack.push(syStack.pop());
    }
}

逆波兰表达式计算

有了逆波兰表达式树求值就非常简单了，想象一下刚才提到的二叉树，先求左子树的值，再求右子树值，然后根据根节点的运算符逐步计算最终的值。需要再创建一个栈模拟逆波兰表达式，遇见数进行入栈，遇见符号将栈中最近的两个数出栈进行操作后再入栈，最后就剩下一个数，就是最后的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function solve( s ) {
    let calStack = [];
    for (let ele of stack) {
        if (ele === '+' || ele === '-' || ele === '*') {
            let num2 = calStack.pop();
            let num1 = calStack.pop();
            let res;
            switch (ele) {
                case '+':
                    res = num1 + num2;
                    break;
                case '-':
                    res = num1 - num2;
                    break;
                case '*':
                    res = num1 * num2;
                    break;
            }
            calStack.push(res);
        } else {
            calStack.push(parseInt(ele));
        }
    }
    return calStack[0];
}

完整代码

将两个步骤组合起来，可以实现最后的结果了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 * 返回表达式的值
 * @param s string字符串 待计算的表达式
 * @return int整型
 */
function solve( s ) {
    // write code here
    // 中缀转后缀
    let stack = [];
    let syStack = [];
    let num = "";
    for (let char of s) {
        if (char >= '0' && char <= '9') {
            num += char;
        } else if (char === '(') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            syStack.push(char);
        } else if (char === '+' || char === '-') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] !== '(') {
                stack.push(syStack.pop());
            }
            syStack.push(char);
        } else if (char === '*') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] === '*') {
                stack.push(syStack.pop());
            }
            syStack.push(char);
        } else if (char === ')') {
            if (num !== '') {
                stack.push(num);
                num = '';
            }
            while (syStack.length && syStack[syStack.length - 1] !== '(') {
                stack.push(syStack.pop());
            }
            syStack.pop();
        }
    }
    if (num !== '') {
        stack.push(num);
    }
    while (syStack.length) {
        stack.push(syStack.pop());
    }
    let calStack = [];
    for (let ele of stack) {
        if (ele === '+' || ele === '-' || ele === '*') {
            let num2 = calStack.pop();
            let num1 = calStack.pop();
            let res;
            switch (ele) {
                case '+':
                    res = num1 + num2;
                    break;
                case '-':
                    res = num1 - num2;
                    break;
                case '*':
                    res = num1 * num2;
                    break;
            }
            calStack.push(res);
        } else {
            calStack.push(parseInt(ele));
        }
    }
    return calStack[0];
}
module.exports = {
    solve : solve
};
-------------本文结束感谢您的阅读-------------

欢迎关注我的其它发布渠道