hxy的博客

Mia san Mia!

0%

BFS、DFS 回溯法刷题

发表于 更新于 分类于 Valine：

按照算法和数据结构进行分类，一起来刷题，用于自己在面试前查漏补缺。我的意向岗位是前端，选择用javascript来刷题，优点是动态语言，语法简单，缺点是遇见复杂数据结构会出现较难的写法，如堆、并查集，每题对应leetcode的题号。本篇是BFS、DFS 回溯法

专题部分

BFS、DFS 回溯法

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

示例 1：

1
2
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

1
2
输入：digits = ""
输出：[]

示例 3：

1
2
输入：digits = "2"
输出：["a","b","c"]

提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 ['2', '9'] 的一个数字。

使用回溯发怎么保存结果，可以数组保存路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @param {string} digits
 * @return {string[]}
 */
let letterMap = [ 
    " ",    // 0
    "",     // 1
    "abc",  // 2
    "def",  // 3
    "ghi",  // 4
    "jkl",  // 5
    "mno",  // 6
    "pqrs", // 7
    "tuv",  // 8
    "wxyz"  // 9
];
var letterCombinations = function(digits) {
    if (digits.length === 0) return [];
    let res = [];
    let aux = [];
    let len = digits.length;
    function backTrack (index) {
        if (index === len) {
            res.push([...aux].join(''));
            return;
        }
        let digit = digits[index];
        let string = letterMap[digit];
        for(let i = 0 ; i < string.length ; i++) {
            aux.push(string[i]);
            backTrack(index + 1);
            aux.pop();
        }
    }
    backTrack(0);
    return res;
};

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

1
2
输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

1
2
输入：n = 1
输出：["()"]

提示：

  • 1 <= n <= 8

同时记录(和)的数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @param {number} n
 * @return {string[]}
 */
var generateParenthesis = function(n) {
    if (n == 0) return [];
    // 记录所有合法的括号组合
    let res = [];
    // 回溯过程中的路径
    let track = "";
    // 可用的左括号和右括号数量初始化为 n
    trackback(n, n, track, res);
    return res;
};

function trackback (left, right, track, res){
    // 若左括号剩下的多，说明不合法
    if (right < left) return;
    // 数量小于 0 肯定是不合法的
    if (left < 0 || right < 0) return;
    // 当所有括号都恰好用完时，得到一个合法的括号组合
    if (left === 0 && right === 0){
        res.push(track);
        return;
    }
   // 尝试放一个左括号
   // 选择
    trackback(left - 1, right, track + '(', res);
    // 撤消选择

    // 尝试放一个右括号
    // 选择
    trackback(left, right - 1, track + ')', res);
    // 撤消选择
};

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

1
2
3
4
5
6
输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
  [7],
  [2,2,3]
]

示例 2：

1
2
3
4
5
6
7
输入：candidates = [2,3,5], target = 8,
所求解集为：
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

提示：

  • 1 <= candidates.length <= 30
  • 1 <= candidates[i] <= 200
  • candidate 中的每个元素都是独一无二的。
  • 1 <= target <= 500

保留完成的路径，需要剪枝优化路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function(candidates, target) {
    let res = [], cur = [];
    // 从小到大排序，方便剪枝
    candidates.sort((a, b) => a - b);
    dfs(target, 0);
    return res;
    // residue，剩下的树，begin开始的位置
    function dfs(residue, begin){
        if(residue === 0){
            res.push([...cur]);
            return ;
        }
        for(let i = begin; i < candidates.length; i++){
            if(residue - candidates[i] < 0){
                return;
            }
            // 加入当前的树
            cur.push(candidates[i]);
            // DFS
            dfs(residue - candidates[i], i);
            // 撤回
            cur.pop();
        }
    }
};

写得完整一些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function(candidates, target) {
    let res = [];
    let len = candidates.length;
    candidates.sort((a, b) => a - b);
    dfs(candidates, len, target, 0, [], res);
    return res;
};
 /**
 * @param candidates 数组输入
 * @param len        输入数组的长度，冗余变量
 * @param residue    剩余数值
 * @param begin      本轮搜索的起点下标
 * @param path       从根结点到任意结点的路径
 * @param res        结果集变量
 */
function dfs(candidates, len, residue, begin, path, res) {
    if (residue == 0) {
        // 由于 path 全局只使用一份，到叶子结点的时候需要做一个拷贝
        res.push([...path]);
        return;
    }
    for (let i = begin; i < len; i++) {
        // 在数组有序的前提下，剪枝
        if (residue < candidates[i]) break;

        // 回溯
        path.push(candidates[i]);
        dfs(candidates, len, residue - candidates[i], i, path, res);
        path.pop();
    }
}

46. 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

1
2
3
4
5
6
7
8
9
10
输入: [1,2,3]
输出:
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

直接用track记录路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
/* 主函数，输入一组不重复的数字，返回它们的全排列 */
var permute = function(nums) {
    const res = [];

    // 记录「路径」
    const track = [];
    const n = nums.length;
    const isVisited = new Array(n).fill(false);
    backtrack(nums, track);
    return res;

    // 路径：记录在 track 中
    // 选择列表：nums 中不存在于 track 的那些元素
    // 结束条件：nums 中的元素全都在 track 中出现
    function backtrack (nums, track){
        // 触发结束条件
        if (track.length === n){
            res.push([...track]);
            return;
        }
        for (let i = 0; i < n; i++){
            // 排除不合法的选择
            if (!isVisited[i]){
                // 做选择
                isVisited[i] = true;
                track.push(nums[i]);
                // 进入下一层决策树
                backtrack(nums, track);
                // 取消选择
                isVisited[i] = false;
                track.pop();
            }
        }
    }
};

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

1
2
3
4
5
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

注意通过排序和跳过相同的数进行剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function(nums) {
    /**
     * 回溯法
     * backtrack 解题题公式
     */
    const res = [];
    const len = nums.length;
    const used = new Array(len);
    // 升序排序
    nums.sort((a, b) => a - b);

    function dfs (path) {
        // 个数选够了
        if (path.length === len) {
            // path的拷贝 加入解集
            res.push([...path]);
            // 结束当前递归 结束当前分支
            return;
        }

        // 枚举出所有的选择
        for (let i = 0; i < len; i++) {
            // 避免产生重复的排列
            if (nums[i - 1] === nums[i] && i - 1 >= 0 && !used[i - 1]) continue;
            // 这个数使用过了，跳过。
            if (used[i]) continue;
            // make a choice
            path.push(nums[i]);
            // 记录路径上做过的选择
            used[i] = true;
            // explore，基于它继续选，递归
            dfs(path);
            // undo the choice
            path.pop();
            // 也要撤销一下对它的记录
            used[i] = false;
        }
    };

    dfs([]);
    return res;
};

51. N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

img

1
2
3
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

1
2
输入：n = 1
输出：[["Q"]]

提示：

  • 1 <= n <= 9
  • 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    let res = [];
    backtrack(n, []);
    return res;

    function backtrack(n, tmp) {
        if (tmp.length === n) {
            let arr = [];
            for (let i = 0; i < n; i++) {
                arr[i] = ".".repeat(tmp[i]) + "Q" + ".".repeat(n - tmp[i] - 1);
            }
            res.push(arr);
        }
        for (let j = 0; j < n; j++) {
            if (isValid(tmp, j)) {
                tmp.push(j);
                backtrack(n, tmp);
                tmp.pop();
            }
        }
    }
    function isValid(arr, j) {
        let i = arr.length;
        for (let x = 0; x < i; x++) {
            let y = arr[x];
            if  (y === j || x + y === i + j || x - y === i - j) return false;
        }
        return true;
    }
};

回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var solveNQueens = function(n) {
    let res = [];
    dfs([], 0);
    return res;
    // 递归调用，初始为空数组（每行皇后的列位置），从第0行开始
    function dfs (subRes, row) {
        if(row === n) {
            // 将每行展开为..Q..形式
            return res.push(subRes.map(i => '.'.repeat(i) + 'Q' + '.'.repeat(n - i -1)));
        }

        // 遍历每一列，使得目前行数的皇后在第col列 
        for (let col = 0; col < n; col++ ) {
            // 遍历数组使得皇后不互相攻击
            if(!subRes.some((j, k) => (j === col || Math.abs(j - col) === Math.abs(k - row)))) {
                // 执行操作
                subRes.push(col);
                // 回溯
                dfs(subRes, row + 1);
                // 撤回
                subRes.pop();
            }
        }
    }
};

52. N皇后 II

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

示例 1：

img

1
2
3
输入：n = 4
输出：2
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

1
2
输入：n = 1
输出：1

提示：

  • 1 <= n <= 9
  • 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/**
 * @param {number} n
 * @return {number}
 */
var totalNQueens = function(n) {
    let res = 0;
    backtrack(n, []);
    return res;

    function backtrack(n, tmp) {
        if (tmp.length === n) {
            // 已回溯到最后一行，找到一种方案
            res++;
            return;
        }
        // 尝试当前行放入第j列
        for (let j = 0; j < n; j++) {
            // 如果可行，放入当前列
            if (isValid(tmp, j)) {
                // 记录当前选择
                tmp.push(j);
                // 继续下一次递归
                backtrack(n, tmp);
                // 撤销当前选择
                tmp.pop();
            }
        }

    }
    // 判断当前列是否有效
    function isValid(arr, col) {
        let len = arr.length;
        for (let x = 0; x < len; x++) {
            let y = arr[x];
            if (y === col || x - y === len - col || x + y === col + len) return false;
        }
        return true;
    }
};

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

1
2
输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10
  • nums 中的所有元素 互不相同

回溯法，遍历各种可行方法，路径重复剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 数学归纳法
var subsets = function(nums) {
    const res = [];

    // 记录「路径」
    const track = [];
    backtrack(nums, 0, track);
    return res;

    function backtrack (nums, start, track){
        res.push(track);
        
        for (let i = start; i < nums.length; i++){
            // 排除不合法的选择
            if (!track.includes(nums[i])){
                // 做选择
                track.push(nums[i]);
                // 进入下一层决策树
                backtrack(nums, i + 1, [...track]);
                // 取消选择
                track.pop();
            }
        }
    }
};

数学归纳法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 数学归纳法
var subsets = function(nums) {
    // base case，返回一个空集
    if (nums.length === 0) return [[]];
    let n = nums.pop();
    // 先递归算出前面元素的所有子集
    let res = subsets(nums);

    let len = res.length;
    for (let i = 0; i < len; i++) {
        // 然后在之前的结果之上追加
        res.push([...res[i], n]);
    }
    return res;
};

将上述数学归纳法中的递归改为回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/**
 * @param {number[]} nums
 * @return {number[][]}
 */
// 数学归纳法
var subsets = function(nums) {
    let res = [[]];
    for(let i = 0; i < nums.length; i++){
        for(let j = 0, len = res.length; j < len; j++){
            res.push(res[j].concat(nums[i]));
        }
    }
    return res;
};

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

img

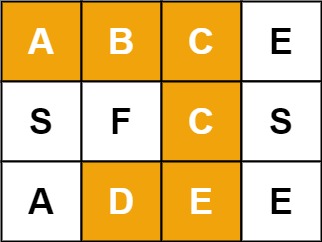
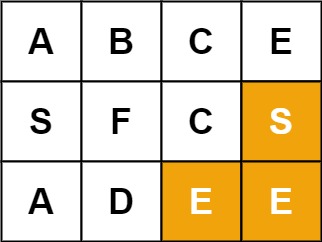
1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

img

1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

img

1
2
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board 和 word 仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    if (board.length === 0 || board[0].length === 0) return false;
    if (word.length === 0) return true;
    let row = board.length;
    let col = board[0].length;
    for (let i = 0; i < row; i ++) {
        for (let j = 0; j < col; j++) {
            // 存在一个序列即返回true
            if (backtrack(i, j, 0)) return true;
        }
    }
    return false;
    // 行，列，当前索引
    function backtrack(i, j, index) {
        if(i >= row || i < 0 || j >= col || j < 0) return false;
        const cur = board[i][j];
        if (cur !== word[index]) return false;
        if (index === word.length - 1) return true;
        // 该位置的数对应单次的当前索引
        // 修改当前节点状态
        board[i][j] = 0;
        // 利用短路效应剪枝回溯
        const res = backtrack(i + 1, j, index + 1) || backtrack(i - 1, j, index + 1) || backtrack(i, j + 1, index + 1) || backtrack(i, j - 1, index + 1);
        // 回改当前节点状态
        board[i][j] = cur;
        return res;
    }
};

当然也可以用额外的空间存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    const m = board.length;
    const n = board[0].length;
    // 二维矩阵used
    const used = new Array(m);
    for (let i = 0; i < m; i++) {
        used[i] = new Array(n);
    }
    // 判断当前点是否是目标路径上的点
    function canFind (row, col, i) {
        // row col是当前点的坐标，i是当前考察的字符索引
        // 递归的出口
        if (i > word.length - 1) {  
            return true;
        }
        // 当前点要存在
        if (row < 0 || row >= m || col < 0 || col >= n) { 
            return false;
        }
        // 当前的点已经走过，或当前点就不是目标点
        if (used[row][col] || board[row][col] != word[i]) { 
            return false;
        }
        // 排除掉这些false情况，当前点是没问题的，可以继续递归考察
        // used记录一下当前点被访问了
        used[row][col] = true; 
        const canFindRest =
            canFind(row + 1, col, i + 1) ||
            canFind(row - 1, col, i + 1) ||
            canFind(row, col + 1, i + 1) ||
            canFind(row, col - 1, i + 1); 
        // 基于当前点，可以为剩下的字符找到路径
        if (canFindRest) { 
            return true;    
        }
        // 找不出，返回false，继续考察别的分支，并撤销当前点的访问状态。
        used[row][col] = false; 
        return false;
    };

    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            // 找到dfs的起点
            if (board[i][j] == word[0] && canFind(i, j, 0)) {
                // 找到起点，且dfs的结果也true，则找到了目标路径
                return true;
            }
        }
    }
    // 怎么样都没有返回true，则返回false
    return false;
};

200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1

示例 2：

1
2
3
4
5
6
7
输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 300
  • grid[i][j] 的值为 '0' 或 '1'

DFS深度优先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function(grid) {
    let row = grid.length;
    if(!row) return 0;
    let col = grid[0].length;
    let res = 0;
    // DFS，将连在一起的几个 ‘1’全部转为‘0’
    function DFS(grid, r, c){
        grid[r][c] = '0';
        if(r - 1 >= 0 && grid[r - 1][c] === '1') DFS(grid, r - 1, c);
        if(r + 1 < row && grid[r + 1][c] === '1') DFS(grid, r + 1, c);
        if(c - 1 >= 0 && grid[r][c - 1] === '1') DFS(grid, r, c - 1);
        if(c + 1 < col && grid[r][c + 1] ==='1') DFS(grid, r, c + 1);
    }

    for(let i = 0; i < row; i++){
        for(let j = 0; j < col; j++){
            if(grid[i][j] === '1'){
                res++;
                DFS(grid, i, j);
            }
        }
    }
    return res;
};

BFS广度优先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @param {character[][]} grid
 * @return {number}
 */
var numIslands = function(grid) {
    if (grid.length === 0) return 0;
    let lenx = grid.length;
    let leny = grid[0].length;
    let num_islands = 0;
    for(let i = 0; i < lenx; i++) {
        for(let j = 0; j < leny; j++){
            if (grid[i][j] === 1) {
               num_islands++;
               grid[i][j] = 0;
               neighbors = new Array();
               neighbors.push([i, j]);
               while (neighbors.length !== 0){
                   let x = neighbors[0][0];
                   let y = neighbors[0][1];
                   if (x - 1 >= 0 && grid[x - 1][y] === 1) {
                        neighbors.push([x - 1, y]);
                        grid[x - 1][y] = 0;
                    }
                    if (x + 1 < lenx && grid[x + 1][y] === 1) {
                        neighbors.push([x + 1, y]);
                        grid[x + 1][y] = 0;
                    }
                    if (y - 1 >= 0 && grid[x][y - 1] === 1) {
                        neighbors.push([x, y - 1]);
                        grid[x][y - 1] = 0;
                    }
                    if (y + 1 < leny && grid[x][y + 1] === 1) {
                        neighbors.push([x, y + 1]);
                        grid[x][y + 1] = 0;
                    }
                    neighbors.shift();
               }
            }
        }
    }
    return num_islands;
};

207. 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

  • 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

  • 1 <= numCourses <= 105
  • 0 <= prerequisites.length <= 5000
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • prerequisites[i] 中的所有课程对互不相同

邻接表+BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function(numCourses, prerequisites) {
    const inDegree = new Array(numCourses).fill(0);
    // 邻接表
    let graph = {};
    for (let i = 0; i < prerequisites.length; i++) {
        // 计算课对应的入度
        inDegree[prerequisites[i][0]]++;
        // 当前课已经存在于邻接表
        if (graph[prerequisites[i][1]]) {
            // 对应的数组新推入依赖它的课
            graph[prerequisites[i][1]].push(prerequisites[i][0]);
        } else { // 当前课不存在于邻接表
            // 推入依赖它的课
            graph[prerequisites[i][1]] = [prerequisites[i][0]];
        }
    }
    // BFS需要的队列
    const queue = [];
    // 初始推入所有入度0的课
    for (let i = 0; i < inDegree.length; i++) {
        if (inDegree[i] === 0) queue.push(i);
    }
    while(queue.length) {
        // 可选的课，出栈
        const select = queue.shift();
        // 获取这门课对应的后续课
        const toEnQueue = graph[select];
        // 确实有后续课
        if (toEnQueue && toEnQueue.length) {
            for (let i in toEnQueue) {
                // 依赖它的后续课的入度-1
                inDegree[toEnQueue[i]]--;
                // 如果因此减为0，入列
                if (inDegree[toEnQueue[i]] === 0) {
                    // 这门课入列
                    queue.push(toEnQueue[i]);
                }
            }
        }
    }
    for (let i in inDegree) {
        // 还有课的入度不为0
        if (inDegree[i] !== 0) return false;
    }
    return true;
};

301. 删除无效的括号

给你一个由若干括号和字母组成的字符串 s ，删除最小数量的无效括号，使得输入的字符串有效。

返回所有可能的结果。答案可以按 任意顺序 返回。

示例 1：

1
2
输入：s = "()())()"
输出：["(())()","()()()"]

示例 2：

1
2
输入：s = "(a)())()"
输出：["(a())()","(a)()()"]

示例 3：

1
2
输入：s = ")("
输出：[""]

提示：

  • 1 <= s.length <= 25
  • s 由小写英文字母以及括号 '(' 和 ')' 组成
  • s 中至多含 20 个括号

回溯法/DFS/暴力
需要解决几个关键点。

第一，怎么判断括号是否匹配？

[20 题](https://leetcode.wang/leetCode-20-Valid Parentheses.html) 的时候做过括号匹配的问题，除了使用栈，我们也可以用一个计数器 count，遇到左括号进行加 1 ，遇到右括号进行减 1，如果最后计数器是 0，说明括号是匹配的。

第二，如果用暴力的方法，怎么列举所有情况？

要列举所有的情况，每个括号无非是两种状态，在或者不在，字母的话就只有「在」一种情况。我们可以通过回溯法或者说是 DFS 。可以参考下边的图。

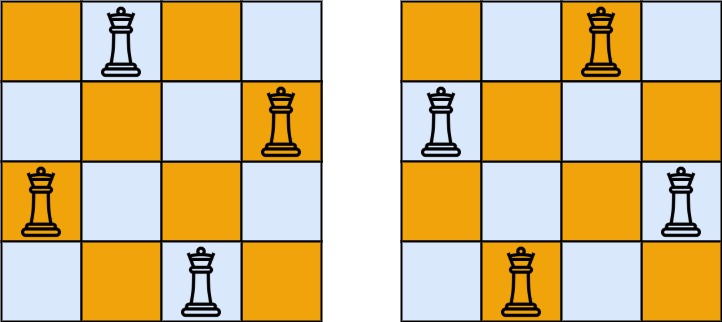
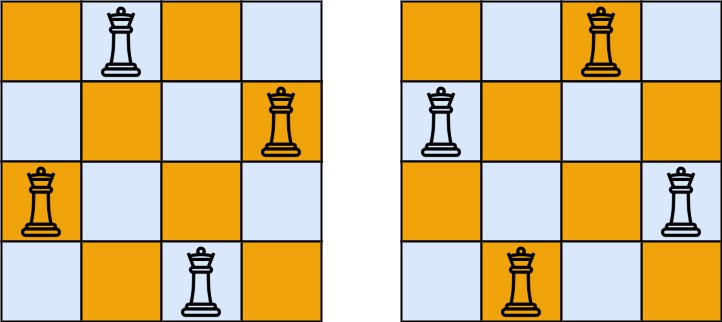
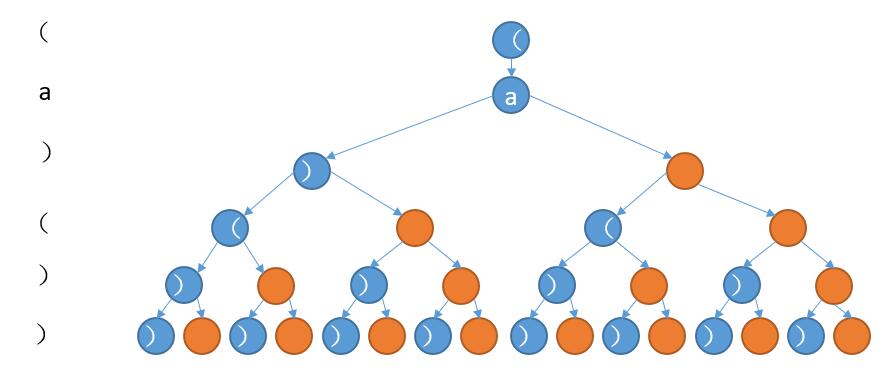
对于 (a)())， 如下图，蓝色表示在，橙色表示不在，下边是第一个字符在的情况。

img

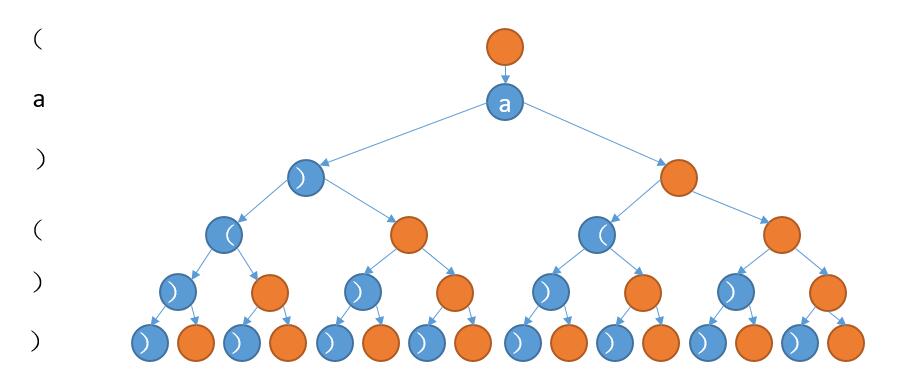
下边是第一个字符不在的情况。

img

我们要做的就是从第一个字符开始，通过深度优先遍历的顺序，遍历到最后一个字符后判断当前路径上的字符串是否合法。

对于代码的话，我们可以一边遍历，一边记录当前 count 的情况，也就是左右括号的情况。到最后一个字符后，只需要判断 count 是否为 0 即可。

第三，怎么保证删掉最少的括号？

这个方法很多，说一下我的。假设我们用 res 数组保存最终的结果，当新的字符串要加入的时候，我们判断一下新加入的字符串的长度和数组中第一个元素长度的关系。

如果新加入的字符串的长度大于数组中第一个元素的长度，我们就清空数组，然后再将新字符串加入。

如果新加入的字符串的长度小于数组中第一个元素的长度，那么当前字符串抛弃掉。

如果新加入的字符串的长度等于数组中第一个元素的长度，将新字符串加入到 res 中。

第四，重复的情况怎么办？

简单粗暴一些，最后通过 set 去重即可。

上边四个问题解决后，就可以写代码了。

因为我们考虑的是删除最少的括号数，我们可以在深度优先遍历之前记录需要删除的左括号的个数和右括号的个数，遍历过程中如果删除的超过了需要删除的括号个数，就可以直接结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/**
 * @param {string} s
 * @return {string[]}
 */
var removeInvalidParentheses = function (s) {
    let res = [''];
    removeInvalidParenthesesHelper(s, 0, s.length, 0, '', res);
    // 去重
    return [...new Set(res)];
};

/**
 * 
 * @param {string 原字符串} s 
 * @param {number 当前考虑的字符下标} start 
 * @param {number s 的长度} end 
 * @param {number 记录左括号和右括号的情况} count 
 * @param {string 遍历的路径字符串} temp 
 * @param {string[] 保存最终的结果} res 
 */
function removeInvalidParenthesesHelper(s, start, end, count, temp, res) {
    // 当前右括号多了, 后边无论是什么都不可能是合法字符串了, 直接结束
    if (count < 0) {
        return;
    }
    // 到达结尾
    if (start === end) {
        if (count === 0) {
            let max = res[0].length;
            if (temp.length > max) {
                // 清空之前的
                res.length = 0;
                // 将当前的加入
                res.push(temp);
            } else if (temp.length === max) {
                res.push(temp);
            }
        }
        return;
    }
    // 添加当前字符
    if (s[start] === '(') {
        removeInvalidParenthesesHelper(
            s,
            start + 1,
            end,
            count + 1,
            temp + '(',
            res
        );
    } else if (s[start] === ')') {
        removeInvalidParenthesesHelper(
            s,
            start + 1,
            end,
            count - 1,
            temp + ')',
            res
        );
    } else {
        removeInvalidParenthesesHelper(
            s,
            start + 1,
            end,
            count,
            temp + s.charAt(start),
            res
        );
    }

    // 不添加当前字符
    if (s[start] === '(' || s[start] === ')') {
        removeInvalidParenthesesHelper(s, start + 1, end, count, temp, res);
    }
}

BFS

思想很简单，先判断整个字符串是否合法， 如果合法的话就将其加入到结果中。否则的话，进行下一步。

只删掉 1 个括号，考虑所有的删除情况，然后判断剩下的字符串是否合法，如果合法的话就将其加入到结果中。否则的话，进行下一步。

只删掉 2 个括号，考虑所有的删除情况，然后判断剩下的字符串是否合法，如果合法的话就将其加入到结果中。否则的话，进行下一步。

只删掉 3 个括号，考虑所有的删除情况，然后判断剩下的字符串是否合法，如果合法的话就将其加入到结果中。否则的话，进行下一步。

…

因为我们考虑删除最少的括号数，如果上边某一步出现了合法情况，后边的步骤就不用进行了。

同样要解决重复的问题，除了解法一在最后返回前用 set 去重。这里我们也可以在过程中使用一个 set ，在加入队列之前判断一下是否重复。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * @param {string} s
 * @return {string[]}
 */
var removeInvalidParentheses = function (s) {
    let res = [];
    let queue = [];

    queue.push([s, 0]);
    
    while (queue.length > 0) {
        s = queue.shift();
        if (isVaild(s[0])) {
            res.push(s[0]);
        } else if (res.length === 0) {
            let removei = s[1];
            s = s[0];
            for (; removei < s.length; removei++) {
                if (
                    // 保证是连续括号的第一个
                    (s[removei] === '(' || s[removei] === ')') &&
                    (removei === 0 || s[removei - 1] != s[removei])
                ) {
                    let nexts = s.substring(0, removei) + s.substring(removei + 1);
                    // 此时删除位置的下标 removei 就是下次删除位置的开始
                    queue.push([nexts, removei]);
                }
            }
        }
    }
    return res;
};

function isVaild(s) {
    let count = 0;
    for (let i = 0; i < s.length; i++) {
        if (s[i] === '(') {
            count++;
        } else if (s[i] === ')') {
            count--;
        }
        if (count < 0) {
            return false;
        }
    }
    return count === 0;
}

399. 除法求值

给你一个变量对数组 equations 和一个实数值数组 values 作为已知条件，其中 equations[i] = [Ai, Bi] 和 values[i] 共同表示等式 Ai / Bi = values[i] 。每个 Ai 或 Bi 是一个表示单个变量的字符串。

另有一些以数组 queries 表示的问题，其中 queries[j] = [Cj, Dj] 表示第 j 个问题，请你根据已知条件找出 Cj / Dj = ? 的结果作为答案。

返回 所有问题的答案 。如果存在某个无法确定的答案，则用 -1.0 替代这个答案。如果问题中出现了给定的已知条件中没有出现的字符串，也需要用 -1.0 替代这个答案。

注意：输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况，且不存在任何矛盾的结果。

示例 1：

1
2
3
4
5
6
输入：equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
输出：[6.00000,0.50000,-1.00000,1.00000,-1.00000]
解释：
条件：a / b = 2.0, b / c = 3.0
问题：a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
结果：[6.0, 0.5, -1.0, 1.0, -1.0 ]

示例 2：

1
2
输入：equations = [["a","b"],["b","c"],["bc","cd"]], values = [1.5,2.5,5.0], queries = [["a","c"],["c","b"],["bc","cd"],["cd","bc"]]
输出：[3.75000,0.40000,5.00000,0.20000]

示例 3：

1
2
输入：equations = [["a","b"]], values = [0.5], queries = [["a","b"],["b","a"],["a","c"],["x","y"]]
输出：[0.50000,2.00000,-1.00000,-1.00000]

提示：

  • 1 <= equations.length <= 20
  • equations[i].length == 2
  • 1 <= Ai.length, Bi.length <= 5
  • values.length == equations.length
  • 0.0 < values[i] <= 20.0
  • 1 <= queries.length <= 20
  • queries[i].length == 2
  • 1 <= Cj.length, Dj.length <= 5
  • Ai, Bi, Cj, Dj 由小写英文字母与数字组成

并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
/**
 * @param {string[][]} equations
 * @param {number[]} values
 * @param {string[][]} queries
 * @return {number[]}
 * 并查集
 */
var calcEquation = function(equations, values, queries) {
    // 父集 存储变量之间的映射关系
    let parentMap = new Map();
    // 存储各个变量之间的比例关系
    let valueMap = new Map();
    // 遍历每个等式，构造并查集
    for (let i = 0; i < equations.length; i++) {
        // 预处理
        // 本身未有的数，设为自己的根节点
        if (!parentMap.has(equations[i][0])) {
            parentMap.set(equations[i][0], equations[i][0]);
        }
        if (!parentMap.has(equations[i][1])) {
            parentMap.set(equations[i][1], equations[i][1]);
        }
        // 本身未有的数，权重初始化为1
        if (!valueMap.has(equations[i][0])) {
            valueMap.set(equations[i][0], 1);
        }
        if (!valueMap.has(equations[i][1])) {
            valueMap.set(equations[i][1], 1);
        }
        // 家里并查集
        union(parentMap, valueMap, equations[i][0], equations[i][1], values[i]);
    }
    // 结果
    const result = [];
    // 根据问题进行查询
    for (let i = 0; i < queries.length; i++) {
        // 查找两数
        let tmp1 = find(parentMap, valueMap, queries[i][0]);
        let tmp2 = find(parentMap, valueMap, queries[i][1]);
        // 未找到两数之一
        if (!tmp1 || !tmp2) {
            result.push(-1.0);
            continue;
        }
        if (tmp1.index === tmp2.index) {
            // 在同一个并查集中
            result.push(tmp1.value / tmp2.value);
        } else {
            // 不在同一个并查集中
            result.push(-1.0);
        }
    }
    return result;
};
// 合并index1和index2对应的集
function union(parentMap, valueMap, index1, index2, value) {
    let tmp1 = find(parentMap, valueMap, index1);
    let tmp2 = find(parentMap, valueMap, index2);
    parentMap.set(tmp1.index, tmp2.index);
    valueMap.set(tmp1.index, (value * tmp2.value) / tmp1.value);
}

function find(parentMap, valueMap, index) {
    let value = 1;
    while (parentMap.get(index) && parentMap.get(index) !== index) {
        value *= valueMap.get(index);
        index = parentMap.get(index);
    }
    if (!parentMap.get(index)) {
        return null;
    }
    return {
        index,
        value
    };
}

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/**
 * @param {string[][]} equations
 * @param {number[]} values
 * @param {string[][]} queries
 * @return {number[]}
 * 深度优先遍历
 */
 var calcEquation = function(equations, values, queries) {
    // 结果
    let res = [];
    // 已经访问过
    let already = [];
    // 判断是否访问过
    let visited = new Array(values.length).fill(false);
    // 遍历所有等式
    for(let item of equations){
        // 没有访问过该数
        if(already.indexOf(item[0]) === -1) already.push(item[0]);
        if(already.indexOf(item[1]) === -1) already.push(item[1]);
    }
    for (let item of queries) {
        // 找不到其中的数
        if (already.indexOf(item[0]) === -1 || already.indexOf(item[1]) === -1)
            res.push(-1.0);
        // 相等的数
        else if (item[0] === item[1])
            res.push(1.0);
        else {
            // let visited=new Array(values.length).fill(false);
            res.push(backtracking(visited, 0, item[0], item[1])[0]);
        }
    }
    return res;
    function backtracking(visited, i, head, tail){
        let ans = [1.0, false];
        if (i === values.length) return [-1.0, false];
        for(let j = 0, len = values.length; j < len; j++){
            if (equations[j][0] === tail && equations[j][1] === head){
                ans[0] *= 1 / values[j];
                return [ans[0], true];
            }
            if((equations[j][0] !== head && equations[j][1] !== head) || visited[j]) continue;

            visited[j] = true;
            let store = ans[0];
            ans[0] *= equations[j][0] === head ? values[j] : 1 / values[j];
            if(equations[j][1] === tail){
                 visited[j] = false;
                 return [ans[0], true];
            }
            let [a, f] = equations[j][0] === head ? backtracking(visited, i + 1, equations[j][1], tail): backtracking(visited,i+1,equations[j][0],tail);
            if(f){
                ans[0] *= a;
                visited[j] = false;
                return [ans[0], true];
            }
            ans[0] = store;
            visited[j] = false;
        }
        return [-1.0, false];
    }
}

417. 太平洋大西洋水流问题

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标。

提示：

  1. 输出坐标的顺序不重要
  2. m 和 n 都小于150

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
给定下面的 5x5 矩阵:

  太平洋 ~   ~   ~   ~   ~ 
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

返回:

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] (上图中带括号的单元).

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
var pacificAtlantic = function(matrix) {
    const direction = [-1, 0, 1, 0, -1];
    if (!matrix.length || !matrix[0].length) {
        return [];
    }
    let ans = [];
    let m = matrix.length, n = matrix[0].length;
    // 左上角能到达的点
    let can_reach_p = Array.from(Array(m), () => Array(n).fill(false));
    // 左上角能到达的点
    let can_reach_a = Array.from(Array(m), () => Array(n).fill(false));
    for (let i = 0; i < m; i++) {
        dfs(can_reach_p, i, 0);
        dfs(can_reach_a, i, n - 1);
    }
    for (let i = 0; i < n; i++) {
        dfs(can_reach_p, 0, i);
        dfs(can_reach_a, m - 1, i);
    }
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (can_reach_p[i][j] && can_reach_a[i][j]) {
                ans.push([i, j]);
            }
        }
    }
    return ans; 
    function dfs(can_reach, r, c) {
        if (can_reach[r][c]) {
            return;
        }
        can_reach[r][c] = true;
        let x, y;
        for (let i = 0; i < 4; i++) {
            x = r + direction[i], y = c + direction[i+1];
            if (x >= 0 && x < m && y >= 0 && y < n && matrix[r][c] <= matrix[x][y]) {
                dfs(can_reach, x, y);
            }
        }
    }
};

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
/**
 * @param {number[][]} matrix
 * @return {number[][]}
 */
var pacificAtlantic = function(matrix) {
    if (!matrix || !matrix[0]) return [];
    const m = matrix.length;
    const n = matrix[0].length;


    const flag = Array.from({length: m + 10}, () => new Array(n + 10).fill(0));
    const flag2 = Array.from({length: m + 10}, () => new Array(n + 10).fill(0));

    const bfs = (x, y) => {
        const q = [[x, y]];
        flag[x][y] = 1;
        while (q.length) {
            const c = q.shift();
            // console.log("出队",c,c[0],c[1])
            var cx = c[0];
            var cy = c[1];
            flag[cx][cy] = 1;
            const num = matrix[cx][cy];
         
            var shang = cx - 1 >= 0 ? matrix[cx - 1][cy] : -1;
            var xia = cx + 1 < m ? matrix[cx + 1][cy] : -1;       
            var zuo = cy - 1 >= 0 ? matrix[cx][cy - 1] : -1;
            var you = cy + 1 < n ? matrix[cx][cy + 1] : -1;
          
            if (shang >= num && flag[cx - 1][cy] === 0){
                flag[cx - 1][cy] = 1;
                q.push([cx - 1, cy]);
            }
            if (xia >= num && flag[cx + 1][cy] === 0){
                flag[cx + 1][cy] = 1;
                q.push([cx + 1, cy]);
            }
            if(zuo>=num&&flag[cx][cy-1]==0){
                flag[cx][cy-1] = 1;
                q.push([cx,cy-1]);
            }
            if(you >= num && flag[cx][cy + 1] == 0){
                flag[cx][cy + 1] = 1;
                q.push([cx, cy + 1]);
            }
        }
        
        
    }

    const bfs2 = (x, y) => {
        const q = [[x, y]];
        flag2[x][y] = 1;
        while (q.length) {
            const c = q.shift();
            var cx = c[0];
            var cy = c[1];
            flag2[cx][cy] = 1;
           
            const num = matrix[cx][cy];
            var shang = cx - 1 >= 0 ? matrix[cx - 1][cy] : -1;
            var xia = cx + 1< m ? matrix[cx + 1][cy] :-1;      
            var zuo = cy - 1 >= 0 ? matrix[cx][cy - 1] : -1;
            var you = cy + 1 < n ? matrix[cx][cy + 1] : -1;
            if(shang >= num && flag2[cx - 1][cy] === 0){
                flag2[cx - 1][cy] = 1;
                q.push([cx - 1, cy]);
            }
            if(xia >= num && flag2[cx + 1][cy] === 0){
                flag2[cx + 1][cy] = 1;
                q.push([cx + 1, cy]);
             
            }
            if(zuo >= num && flag2[cx][cy - 1] === 0){
                flag2[cx][cy - 1] = 1;
                q.push([cx, cy - 1]);
            }
            if(you >= num && flag2[cx][cy + 1] === 0){
                flag2[cx][cy + 1] = 1;
                q.push([cx, cy + 1]);
            }
        }
        
        
    }

    for(let i = 0; i < n; i++){
        bfs(0, i);
    }
    for(let i = 0; i < m; i++){
        bfs(i, 0);
    }
    for(let i=0;i<m;i++){
        bfs2(i, n - 1);
    }
    for(let i = 0; i < n; i++){
        bfs2(m - 1, i);
    }
    const qq = [];
    for(let i = 0; i < m; i++){
        for(let j = 0; j < n; j++){
            if(flag[i][j] + flag2[i][j] === 2){
                qq.push([i, j]);
            }
        }
    }
    return qq;
};

547. 省份数量

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

img

1
2
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

img

1
2
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

  • 1 <= n <= 200
  • n == isConnected.length
  • n == isConnected[i].length
  • isConnected[i][j] 为 1 或 0
  • isConnected[i][i] == 1
  • isConnected[i][j] == isConnected[j][i]

DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * @param {number[][]} M
 * @return {number}
 */
var findCircleNum = function(M) {
    let n = M.length;
    if (!n) return 0;
    let count = 0;
    let isVisited = new Array(n).fill(false);
    for (let i = 0; i < n; i++) {
        if (!isVisited[i]) {
            dfs(i);
            count++;
        }
    }
    return count;
    function dfs(i) {
        isVisited[i] = true;
        for (let j = 0; j < n; j++) {
            if (!isVisited[j] && M[i][j]) {
                dfs(j);
            }
        }
    }
};

或者用set存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * @param {number[][]} M
 * @return {number}
 * 深度优先搜索
 */
var findCircleNum = function(M) {
    // 已访问的省份数
    let visited = new Set();
    // 集的个数
    let count = 0;
    // 遍历每行
    for (let i = 0; i < M.length; i++) {
        // 检查第i个城市是否已访问过
        if (!visited.has(i)) {
            // 未访问过i，进行深度遍历搜索
            dfs(M, visited, i);
            count++;
        }
    }
    return count;
}
// 深度优先搜索原矩阵
function dfs(M, visited, i) { 
    // 遍历改行
    for (let j = 0; j < M.length; j++) {
        // i与j联通，且没有访问过
        if (M[i][j] == 1 && !visited.has(j)) {
            visited.add(j);
            dfs(M, visited, j);
        }
    }
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/**
 * @param {number[][]} M
 * @return {number}
 * 广度优先搜索
 */
var findCircleNum = function(M) {
    // 省份数量
    const provinces = M.length;
    // 已遍历的
    const visited = new Set();
    // 图的个数
    let circles = 0;
    // 队列
    const queue = new Array();
    // 遍历各行
    for (let i = 0; i < provinces; i++) {
        // 未访问该省
        if (!visited.has(i)) {
            queue.push(i);
            while (queue.length) {
                // 首页
                const j = queue.shift();
                visited.add(j);
                for (let k = 0; k < provinces; k++) {
                    if (M[j][k] === 1 && !visited.has(k)) {
                        queue.push(k);
                    }
                }
            }
            circles++;
        }
    }
    return circles;
};

并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * @param {number[][]} M
 * @return {number}
 * 并查集
 */
var findCircleNum = function(isConnected) {
    const provinces = isConnected.length;
    const parent = new Array(provinces).fill(0);
    for (let i = 0; i < provinces; i++) {
        parent[i] = i;
    }
    for (let i = 0; i < provinces; i++) {
        for (let j = i + 1; j < provinces; j++) {
            if (isConnected[i][j] == 1) {
                union(parent, i, j);
            }
        }
    }
    let circles = 0;
    for (let i = 0; i < provinces; i++) {
        if (parent[i] === i) {
            circles++;
        }
    }
    return circles;
};
// 并
const union = (parent, index1, index2) => {
    parent[find(parent, index1)] = find(parent, index2);
}

// 查找
const find = (parent, index) => {
    if (parent[index] !== index) {
        parent[index] = find(parent, parent[index]);
    }
    return parent[index];
}

695. 岛屿的最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid 。

一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

找到给定的二维数组中最大的岛屿面积。(如果没有岛屿，则返回面积为 0 。)

示例 1:

1
2
3
4
5
6
7
8
[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11 ，因为岛屿只能包含水平或垂直的四个方向的 1 。

示例 2:

1
[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵, 返回 0。

注意: 给定的矩阵grid 的长度和宽度都不超过 50。

DFS 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function(grid) {
    if (!grid.length) return 0;

    let max = 0;

    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[i].length; j++) {
            if (grid[i][j] === 0) {
                continue;
            }

            max = Math.max(max, dfs(i, j, 1));
        }
    }

    function dfs (i, j, count) {
        if (i < 0 || i > grid.length - 1 || j < 0 || j > grid[i].length - 1) {
            return 0;
        }
        if (grid[i][j] === 0) {
            return 0;
        }
        grid[i][j] = 0;

        let downCount = dfs(i + 1, j);
        let upCount = dfs(i - 1, j);
        let leftCount = dfs(i, j + 1);
        let rightCount = dfs(i, j - 1);

        return 1 + downCount + upCount + leftCount + rightCount;
    }

    return max;
};

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxAreaOfIsland = function(grid) {
    let row = grid.length, col = grid[0].length;
    let direct = [[0, 1], [1, 0], [0, -1], [-1, 0]];
    let stack = [], max = 0;
    for(let i = 0; i < row; i++) {
        for(let j = 0; j < col; j++) {
            if(grid[i][j] === 0) continue;
            let t = 1;
            stack.push([i, j]);
            grid[i][j] = 0;
            while(stack.length > 0) {
                let [x, y] = stack.pop();
                for(let k = 0; k < 4; k++) {
                    let newX = x + direct[k][0];
                    let newY = y + direct[k][1];
                    if(newX >= 0 && newY >= 0 && newX < row && newY < col && grid[newX][newY] === 1) {
                        grid[newX][newY] = 0;
                        stack.push([newX, newY]);
                        t++;
                    }
                }
            }
            max = Math.max(max, t);
        }
    }
    return max;
};

寻找和为定值的多个数

题目描述

输入两个整数n和sum，从数列1，2，3…….n 中随意取几个数，使其和等于sum，要求将其中所有的可能组合列出来。

解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
function getAllCombin(array, n, sum, temp) {
    if (temp.length === n) {
        if (temp.reduce((t, c) => t + c) === sum) {
            return temp;
        }
        return;
    }
    for (let i = 0; i < array.length; i++) {
        const current = array.shift();
        temp.push(current);
        const result = getAllCombin(array, n, sum, temp);
        if (result) {
            return result;
        }
        temp.pop();
        array.push(current);
    }
}
const arr = [1, 2, 3, 4, 5, 6];

console.log(getAllCombin(arr, 3, 10, []));
-------------本文结束感谢您的阅读-------------

欢迎关注我的其它发布渠道