数学计算刷题

按照算法和数据结构进行分类，一起来刷题，用于自己在面试前查漏补缺。我的意向岗位是前端，选择用javascript来刷题，优点是动态语言，语法简单，缺点是遇见复杂数据结构会出现较难的写法，如堆、并查集，每题对应leetcode的题号。本篇是数学计算

专题部分

数学计算

7. 整数反转

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−$$ 2^{31} $$ , $$ 2^{31} − 1$$] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

1 2	输入：x = 123 输出：321

示例 2：

1 2	输入：x = -123 输出：-321

示例 3：

1 2	输入：x = 120 输出：21

示例 4：

1 2	输入：x = 0 输出：0

提示：

$- 2^{31} <= x <= 2^{31} - 1$

不用字符串了，话说小学QB编程就有种题了，需要注意取值范围超过范围值为0

/**
 * @param {number} x
 * @return {number}
 */
var reverse = function(x) {
    if (x === 0) return 0;
    // 正负标志位
    let sign = 1;
    if (x < 0) {
        sign = -1;
        x = -x;
    }
    let xr = 0;
    while (x) {
        xr *= 10;
        xr += x % 10;
        x = Math.floor(x / 10);
    }
    if (xr >= Math.pow(2, 31)) return 0;
    return sign * xr;
};

12. 整数转罗马数字

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给你一个整数，将其转为罗马数字。

示例 1:

1 2	输入: num = 3 输出: "III"

示例 2:

1 2	输入: num = 4 输出: "IV"

示例 3:

1 2	输入: num = 9 输出: "IX"

示例 4:

1
2
3

输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.

示例 5:

1
2
3

输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

1 <= num <= 3999

暴力+哈希，找出千位百位十位个位的表达方法，进行对应位的表达

/**
 * @param {number} num
 * @return {string}
 * 暴力法，找出千位百位十位个位的表达方法
 */
var intToRoman = function(num) {
    const M = ["", "M", "MM", "MMM"]; // 千位
    const C = ["", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"]; // 百位
    const X = ["", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"]; // 十位
    const I = ["", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"]; // 个位
    return M[Math.floor(num / 1000)] + C[Math.floor((num % 1000) / 100)] + X[Math.floor((num % 100) / 10)] + I[num % 10];
};

13. 罗马数字转整数

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。输入确保在 1 到 3999 的范围内。

示例 1:

1 2	输入: "III" 输出: 3

示例 2:

1 2	输入: "IV" 输出: 4

示例 3:

1 2	输入: "IX" 输出: 9

示例 4:

1
2
3

输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.

示例 5:

1
2
3

输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

1 <= s.length <= 15
s 仅含字符 ('I', 'V', 'X', 'L', 'C', 'D', 'M')
题目数据保证 s 是一个有效的罗马数字，且表示整数在范围 [1, 3999] 内
题目所给测试用例皆符合罗马数字书写规则，不会出现跨位等情况。
IL 和 IM 这样的例子并不符合题目要求，49 应该写作 XLIX，999 应该写作 CMXCIX 。
关于罗马数字的详尽书写规则，可以参考罗马数字 - Mathematics 。

关键就是根据定义，前一个数比当前数小，减去前一个数，前一个数大于或等于当前数，加上前一个数

/**
 * @param {string} s
 * @return {number}
 */
var romanToInt = function(s) {
    // 索引
    let map = {
        'I': 1,
        'V': 5,
        'X': 10,
        'L': 50,
        'C': 100,
        'D': 500,
        'M': 1000
    };
    // 结果
    let res = 0;
    // 前一个数
    let pre = map[s[0]];
    for(let i = 1; i < s.length; i++) {
        // 当前的数
        let cur = map[s[i]];
        if (pre < cur) {
            // 前一个数比当前数小，减去前一个数
            res -= pre;
        } else {
            // 前一个数大于或等于当前数，加上前一个数
            res += pre;
        }
        // 当前数的值赋给当前前一个数
        pre = cur;
    }
    // 最后一个数加入结果
    res += pre;
    // 返回结果
    return res;
};

31. 下一个排列

实现获取 下一个排列 的函数，算法需要将给定数字序列重新排列成字典序中下一个更大的排列。

如果不存在下一个更大的排列，则将数字重新排列成最小的排列（即升序排列）。

必须** 原地 **修改，只允许使用额外常数空间。

示例 1：

1 2	输入：nums = [1,2,3] 输出：[1,3,2]

示例 2：

1 2	输入：nums = [3,2,1] 输出：[1,2,3]

示例 3：

1 2	输入：nums = [1,1,5] 输出：[1,5,1]

示例 4：

1 2	输入：nums = [1] 输出：[1]

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 100

从末尾找到第一队逆序数，交换位置靠前的数和比他略大的数，数字后面的数从小到大排列

/**
 * @param {number[]} nums
 * @return {void} Do not return anything, modify nums in-place instead.
 * 从末尾找到第一队逆序数，交换位置靠前的数和比他略大的数，数字后面的数从小到大排列
 */
var nextPermutation = function (nums) {
    if (nums.length <= 1) {
        return;
    }
    let p2 = nums.length - 1;
    let p1 = p2 - 1;
    while (p2 > 0 && nums[p1] >= nums[p2]) {
        p2--;
        p1--;
    }
    if (p2 === 0) {
        // 数字从大打小排列，是最大的数，下一个数从小到大排列
        reverse(nums, 0);
        return;
    } else {
        while (p2 <= nums.length - 1 && nums[p1] < nums[p2]) {
            p2++;
        }
        p2--;
        // 交换位置靠前的数和比他略大的数
        swap(nums, p1, p2);
        // 换完后的数从小到大排列
        reverse(nums, p1 + 1);
    }
    return;
}
// 交换nums数组p1位置和p2位置
function swap(nums, p1, p2) {
    const temp = nums[p2];
    nums[p2] = nums[p1];
    nums[p1] = temp;
}
// nums数组从第index位置开始反转
function reverse(nums, index) {
    const len = nums.length;
    if (index === len || index === len - 1) {
        return;
    }
    // 双指针进行数字的交换
    let p1 = index;
    let p2 = len - 1;
    while (p1 < p2) {
        swap(nums, p1, p2);
        p1++;
        p2--;
    }
}

69. x 的平方根

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

1 2	输入: 4 输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

牛顿迭代法

var mySqrt = function(x) {
    let s = x;
    while (s * s > x) {
        s = (s + x / s) >> 1;
    }
    return s;
}

二分查找

var mySqrt = function(x) {
    if (x === 0) return x;
    let l = 1, r = x, mid, sqrt;
    while (l <= r) {
        mid = l + ((r - l) >> 1);
        sqrt = Math.floor(x / mid);
        if (sqrt === mid) {
            return mid;
        } else if (mid > sqrt) {
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }
    return r;
};

231. 2 的幂

给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

如果存在一个整数 x 使得 $n == 2^{x}$ ，则认为 n 是 2 的幂次方。

示例 1：

1
2
3

输入：n = 1
输出：true
解释：2^0 = 1

示例 2：

1
2
3

输入：n = 16
输出：true
解释：2^4 = 16

示例 3：

1 2	输入：n = 3 输出：false

示例 4：

1 2	输入：n = 4 输出：true

示例 5：

1 2	输入：n = 5 输出：false

提示：

$-2^{31} <= n <= 2^{31} - 1$

进阶：你能够不使用循环/递归解决此问题吗？

位运算，取反之后位与是自身

/**
 * @param {number} n
 * @return {boolean}
 */
var isPowerOfTwo = function(n) {
    return n > 0 && (n & (-n)) === n;
};

位运算，与减一后位与结果为0

/**
 * @param {number} n
 * @return {boolean}
 */
var isPowerOfTwo = function(n) {
    return n > 0 && (n & (n - 1)) === 0;
}

递归

/**
 * @param {number} n
 * @return {boolean}
 */
var isPowerOfTwo = function(n) {
	if (n === 1) return true;
    if (n === 0) return false;
    if (Math.ceil(n) !== n) return false;
    return isPowerOfTwo(n / 2);
};

循环计算

/**
 * @param {number} n
 * @return {boolean}
 */
var isPowerOfTwo = function (n) {
    while (n >= 2) {
    	n = n / 2;
    }

    return !!(n === 1);
};

260. 只出现一次的数字

给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。

进阶：你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

示例 1：

1
2
3

输入：nums = [1,2,1,3,2,5]
输出：[3,5]
解释：[5, 3] 也是有效的答案。

示例 2：

1 2	输入：nums = [-1,0] 输出：[-1,0]

示例 3：

1 2	输入：nums = [0,1] 输出：[1,0]

提示：

2 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
除两个只出现一次的整数外，nums 中的其他数字都出现两次

找到两个数异或结果，根据最低位分别对数据进行抑或操作

function FindNumsAppearOnce( array ) {
    // 抑或结果
    let xor_result = 0;
    // 长度
    const n = array.length;
    for (let i = 0; i < n; i++) {
        xor_result ^= array[i];
    }
    // 除了最后1位1，全部置零
    let flag = xor_result & (-xor_result);
    // 有无标志位
    let has_flag = 0, hasnot_flag = 0;
    for (let i = 0; i < n; i++) {
        if (array[i] & flag) {
            // 标志位为1的抑或结果
            has_flag ^= array[i];
        } else {
            // 标志位为0的抑或结果
            hasnot_flag ^= array[i];
        }
    }
    if (has_flag < hasnot_flag) {
        return [has_flag, hasnot_flag];
    } else {
        return [hasnot_flag, has_flag];
    }
}

338. 比特位计数

给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ，计算其二进制数中的 1 的数目并将它们作为数组返回。

示例 1:

1 2	输入: 2 输出: [0,1,1]

示例 2:

1 2	输入: 5 输出: [0,1,1,2,1,2]

进阶:

给出时间复杂度为O(n*sizeof(integer))**的解答非常容易。但你可以在线性时间O(n)**内用一趟扫描做到吗？
要求算法的空间复杂度为**O(n)**。
你能进一步完善解法吗？要求在C++或任何其他语言中不使用任何内置函数（如 C++ 中的 __builtin_popcount）来执行此操作。

一个一个计算

/**
 * @param {number} num
 * @return {number[]}
 */
var countBits = function(num) {
    let result = [0];
    let n = 1;
    while(n <= num){
        let count = 0;
        let tmpN = n;
        while(tmpN !== 0){
            count++;
            tmpN &= (tmpN - 1);
        }
        result.push(count);
        n++;
    }
    return result;
};

类似动态规划的方案

/**
 * @param {number} num
 * @return {number[]}
 */
var countBits = function(num) {
    let number = [0];
    for (let i = 1; i <= num; i++)
        number[i] = number[i >> 1] + (i & 1);
        // 等价于dp[i] = dp[i & (i - 1)] + 1;
    return number;
};

342. 4的幂

给定一个整数，写一个函数来判断它是否是 4 的幂次方。如果是，返回 true ；否则，返回 false 。

整数 n 是 4 的幂次方需满足：存在整数 x 使得 $n == 4^{x}$

示例 1：

1 2	输入：n = 16 输出：true

示例 2：

1 2	输入：n = 5 输出：false

示例 3：

1 2	输入：n = 1 输出：true

提示：

$-2^{31} <= n <= 2^{31}- 1$

进阶：

你能不使用循环或者递归来完成本题吗？

如果 n 是 4 的幂，那么 n 的二进制表示中有且仅有一个 1，并且这个 1 出现在从低位开始的第偶数个二进制位上（这是因为这个 1 后面必须有偶数个 0）。这里我们规定最低位为第 0 位，例如 n=16 时，n 的二进制表示为$(10000)_2$
唯一的 1 出现在第 4 个二进制位上，因此 n 是 4 的幂。

由于题目保证了 n 是一个 32 位的有符号整数，因此我们可以构造一个整数 $\textit{mask}$，它的所有偶数二进制位都是 0，所有奇数二进制位都是 1。这样一来，我们将 n 和 $\textit{mask}$ 进行按位与运算，如果结果为 0，说明 n 二进制表示中的 1 出现在偶数的位置，否则说明其出现在奇数的位置。

根据上面的思路，$\textit{mask}$ 的二进制表示为：

$$
\textit{mask} = (10101010101010101010101010101010)_2
$$

我们也可以将其表示成 16 进制的形式，使其更加美观：

$$
\textit{mask} = (\text{AAAAAAAA})_{16}
$$

/**
 * @param {number} num
 * @return {boolean}
 */
var isPowerOfFour = function(num) {
    return (num > 0) && (!(num & (num - 1))) && ((num & 0xaaaaaaaa) == 0);
};

如果 n 是 4 的幂，那么它可以表示成$4^{x}$ 的形式，我们可以发现它除以 3 的余数一定为 1，即：
$$
4^x \equiv (3+1)^x \equiv 1^x \equiv 1 \quad (\bmod ~3)
$$
如果 n 是 2 的幂却不是 4 的幂，那么它可以表示成 $4^x \times 2$ 的形式，此时它除以 3 的余数一定为 2。

因此我们可以通过 n 除以 3 的余数是否为 1 来判断 n 是否是 4 的幂。

/**
 * @param {number} num
 * @return {boolean}
 */
var isPowerOfFour = function(num) {
    return (num > 0) && (!(num & (num - 1))) && num % 3 === 1;
};

461. 汉明距离

两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。

给出两个整数 x 和 y，计算它们之间的汉明距离。

注意：
$0 ≤ x, y < 2^{31}$.

示例:

输入: x = 1, y = 4
输出: 2

解释:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑

上面的箭头指出了对应二进制位不同的位置。

将两数异或的结果进行统计1的计数

/**
 * @param {number} x
 * @param {number} y
 * @return {number}
 */
var hammingDistance = function(x, y) {
    let diff = x ^ y, ans = 0;
    while (diff) {
        ans += diff & 1;
        diff >>= 1;
    }
    return ans;
};

简化统计1的方式

/**
 * @param {number} x
 * @param {number} y
 * @return {number}
 */
var hammingDistance = function(x, y) {
    let n = x ^ y;
    let res = 0;
    while (n) {
        res++;
        n = n & (n - 1);
    }
    return res;
};

477. 汉明距离总和

两个整数的汉明距离指的是这两个数字的二进制数对应位不同的数量。

计算一个数组中，任意两个数之间汉明距离的总和。

示例:

输入: 4, 14, 2
输出: 6

解释: 在二进制表示中，4表示为0100，14表示为1110，2表示为0010。（这样表示是为了体现后四位之间关系）
所以答案为：
HammingDistance(4, 14) + HammingDistance(4, 2) + HammingDistance(14, 2) = 2 + 2 + 2 = 6.

注意:

数组中元素的范围为从 0到 10^9。
数组的长度不超过 10^4。

统计每一位1的个数

/**
 * @param {number[]} nums
 * @return {number}
 */
var totalHammingDistance = function (nums) {
    let res = 0;
    const len = nums.length;
    for (let i = 0; i < 32; i++) {
        // 左移，mask第i位为1
        let mask = 1 << i;
        let count = 0;
        // 统计所有数组元素第i位1的个数
        for (let value of nums) {
            if (value & mask) count++;
        }
        res += count * (len - count);
    }
    return res;
}

483. 最小好进制

对于给定的整数 n, 如果n的k（k>=2）进制数的所有数位全为1，则称 k（k>=2）是 n 的一个**好进制**。

以字符串的形式给出 n, 以字符串的形式返回 n 的最小好进制。

示例 1：

1
2
3

输入："13"
输出："3"
解释：13 的 3 进制是 111。

示例 2：

1
2
3

输入："4681"
输出："8"
解释：4681 的 8 进制是 11111。

示例 3：

1
2
3

输入："1000000000000000000"
输出："999999999999999999"
解释：1000000000000000000 的 999999999999999999 进制是 11。

提示：

n的取值范围是 [3, 10^18]。
输入总是有效且没有前导 0,

数学方法计算，选择二分查找增加速度

/**
 * @param {string} n
 * @return {string}
 */
var smallestGoodBase = function(n) {
    n = BigInt(n);
    // 先确定 a 的最大值，因为Math.log2的参数不能是 BigInt，所以只能从小到大去算a的 i 次方
    let a_max;
    for (let i = 1; ; i++) {
        if (Math.pow(2, i) > n) {
            a_max = BigInt(i) + 1n;
            break;
        }
    }
    // console.log("a_max:" + a_max);
    // a 不能等于 1，因为 a 等于 1 的时候，k 就等于 n 了。但是任意给定一个 n，都可以存在k 等于 n-1，a 等于 2，使得题目成立
    for(let a = a_max; a >= 2n; a--) {
        // k >= 2 && k <= n - 1, 可以使用二分查找的方式
        let start = 2n;
        let end = n - 1n;
        let k;
        while (true) {
            k = (start + end) / 2n;
            let result = (k ** a - 1n) / (k - 1n);
            if (result === n) {
                return k.toString();
            } else if (result > n) {
                end = k - 1n;
            } else if (result < n) {
                start = k + 1n;
            }
            if (start > end) break;
        }
    }
};

523. 连续的子数组和

给你一个整数数组 nums 和一个整数 k ，编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组：

子数组大小 至少为 2 ，且
子数组元素总和为 k 的倍数。

如果存在，返回 true ；否则，返回 false 。

如果存在一个整数 n ，令整数 x 符合 x = n * k ，则称 x 是 k 的一个倍数。

示例 1：

1
2
3

输入：nums = [23,2,4,6,7], k = 6
输出：true
解释：[2,4] 是一个大小为 2 的子数组，并且和为 6 。

示例 2：

输入：nums = [23,2,6,4,7], k = 6
输出：true
解释：[23, 2, 6, 4, 7] 是大小为 5 的子数组，并且和为 42 。 
42 是 6 的倍数，因为 42 = 7 * 6 且 7 是一个整数。

示例 3：

1 2	输入：nums = [23,2,6,4,7], k = 13 输出：false

提示：

1 <= nums.length <= 105
0 <= nums[i] <= 109
0 <= sum(nums[i]) <= 231 - 1
1 <= k <= 231 - 1

前缀和+哈希表

/**
 * @param {number[]} nums
 * @param {number} k
 * @return {boolean}
 */
var checkSubarraySum = function(nums, k) {
    let sumMod = 0;
    let map = new Map();
    map.set(0, -1);
    for (let i = 0; i < nums.length; i++) {
        const num = nums[i];
        sumMod = (sumMod + num) % k;
        if (map.has(sumMod)) {
            if (map.get(sumMod) === true || (i - map.get(sumMod) > 1)) {
                return true;
            } else {
                map.set(sumMod, true);
            }
        } else {
            map.set(sumMod, i);
        }
    }
    return false;
};

633. 平方数之和

给定一个非负整数 c ，你要判断是否存在两个整数 a 和 b，使得$a^2 + b^2 = c^2$ 。

示例 1：

1
2
3

输入：c = 5
输出：true
解释：1 * 1 + 2 * 2 = 5

示例 2：

1 2	输入：c = 3 输出：false

示例 3：

1 2	输入：c = 4 输出：true

示例 4：

1 2	输入：c = 2 输出：true

示例 5：

1 2	输入：c = 1 输出：true

提示：

$0 <= c <= 2^{31} - 1$

双指针

/**
 * @param {number} c
 * @return {boolean}
 */
var judgeSquareSum = function(c) {
    let start = 0, end = Math.floor(Math.sqrt(c));
    while (start <= end) {
        let sum = start * start + end * end;
        if (sum === c)
            return true;
        else if (sum > c)
            end--;
        else
            start++;
    }
    return false;
};

810. 黑板异或游戏

黑板上写着一个非负整数数组 nums[i] 。Alice 和 Bob 轮流从黑板上擦掉一个数字，Alice 先手。如果擦除一个数字后，剩余的所有数字按位异或运算得出的结果等于 0 的话，当前玩家游戏失败。 (另外，如果只剩一个数字，按位异或运算得到它本身；如果无数字剩余，按位异或运算结果为 0。）

换种说法就是，轮到某个玩家时，如果当前黑板上所有数字按位异或运算结果等于 0，这个玩家获胜。

假设两个玩家每步都使用最优解，当且仅当 Alice 获胜时返回 true。

示例：

输入: nums = [1, 1, 2]
输出: false
解释: 
Alice 有两个选择: 擦掉数字 1 或 2。
如果擦掉 1, 数组变成 [1, 2]。剩余数字按位异或得到 1 XOR 2 = 3。那么 Bob 可以擦掉任意数字，因为 Alice 会成为擦掉最后一个数字的人，她总是会输。
如果 Alice 擦掉 2，那么数组变成[1, 1]。剩余数字按位异或得到 1 XOR 1 = 0。Alice 仍然会输掉游戏。

提示：

1 <= N <= 1000
0 <= nums[i] <= 2^16

有偶数个数或者所有数字异或结果为0必胜，否则必败（拿掉1个数后变成后手必胜的情况）

/**
 * @param {number[]} nums
 * @return {boolean}
 * 有偶数个数或者所有数字异或结果为0必胜，否则必败（拿掉1个数后变成后手必胜的情况）
 */
var xorGame = function(nums) {
    // 偶数个数
    if (nums.length % 2 === 0) return true;
    // 异或结果
    let xor = nums.reduce((prev, next) => prev ^ next);
    return xor === 0;
};

877. 石子游戏

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。每回合，玩家从行的开始或结束处取走整堆石头。这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

提示：

2 <= piles.length <= 500
piles.length 是偶数。
1 <= piles[i] <= 500
sum(piles) 是奇数。

先看动态规划吧

/**
 * @param {number[]} piles
 * @return {boolean}
 */
var stoneGame = function(piles) {
    const n = piles.length;
    // 初始化 dp 数组
    let dp = [];
    // 填入 base case
    for(let i = 0; i < n; i++){
        dp[i] = new Array(n).fill({fir: 0, sec: 0});
        dp[i][i] = {fir: piles[i], sec: 0};
    }
    for(let i = n - 1; i >= 0; i--){
        for(let j = i + 1; j < n; j++) {
            // 先手选择最左边或最右边的分数
            let left = piles[i] + dp[i + 1][j].sec;
            let right = piles[j] + dp[i][j - 1].sec;
            // 套用状态转移方程
            if(left > right){
                dp[i][j].fir = left;
                dp[i][j].sec = dp[i + 1][j].fir;
            } else {
                dp[i][j].fir = right;
                dp[i][j].sec = dp[i][j - 1].fir;
            }
        }
    }
    // console.log(dp);
    const last = dp[0][n - 1];
    return last.fir - last.sec > 0;
};

说白了小学奥数染色问题

/**
 * @param {number[]} piles
 * @return {boolean}
 */
var stoneGame = function(piles) {
    return true;
};

1074. 元素和为目标值的子矩阵数量

给出矩阵 matrix 和目标值 target，返回元素总和等于目标值的非空子矩阵的数量。

子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。

如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同（如：x1 != x1'），那么这两个子矩阵也不同。

示例 1：

1
2
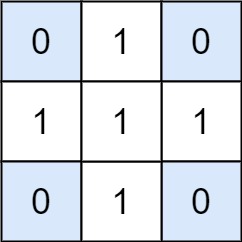
3

输入：matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出：4
解释：四个只含 0 的 1x1 子矩阵。

示例 2：

1
2
3

输入：matrix = [[1,-1],[-1,1]], target = 0
输出：5
解释：两个 1x2 子矩阵，加上两个 2x1 子矩阵，再加上一个 2x2 子矩阵。

示例 3：

1 2	输入：matrix = [[904]], target = 0 输出：0

提示：

1 <= matrix.length <= 100
1 <= matrix[0].length <= 100
-1000 <= matrix[i] <= 1000
-10^8 <= target <= 10^8

我们枚举子矩阵的上下边界，并计算出该边界内每列的元素和，则原问题转换成了如下一维问题：

给定一个整数数组和一个整数target，计算该数组中子数组和等于target 的子数组个数。

对于每列的元素和sum 的计算，我们在枚举子矩阵上边界 i 时，初始下边界 j 为 i，此时 sum 就是矩阵第 i 行的元素。每次向下延长下边界 j 时，我们可以将矩阵第 j 行的元素累加到 sum 中。

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {number}
 * 前缀和+哈希表
 */
var numSubmatrixSumTarget = function(matrix, target) {
    let res = 0;
    // 行数和列数
    const m = matrix.length, n = matrix[0].length;
    // 枚举上边界
    for (let i = 0; i < m; i++) {
        const sum = new Array(n).fill(0);
        // 枚举下边界
        for (let j = i; j < m; j++) {
            // 前缀和
            const prefixSum = new Map();
            prefixSum.set(0, 1);
            // 枚举每列
            for (let k = 0; k < n; k++) {
                // 更新每列的元素和
                sum[k] += matrix[j][k];
            }
            let pre = 0;
            for (const x of sum) {
                pre += x;
                if (prefixSum.has(pre - target)) {
                    res += prefixSum.get(pre - target);
                }
                prefixSum.set(pre, (prefixSum.get(pre) || 0) + 1);
            }
        }
    }
    return res;
};

1310. 子数组异或查询

有一个正整数数组 arr，现给你一个对应的查询数组 queries，其中 queries[i] = [Li, Ri]。

对于每个查询 i，请你计算从 Li 到 Ri 的 XOR 值（即 arr[Li] **xor** arr[Li+1] **xor** ... **xor** arr[Ri]）作为本次查询的结果。

并返回一个包含给定查询 queries 所有结果的数组。

示例 1：

输入：arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
输出：[2,7,14,8] 
解释：
数组中元素的二进制表示形式是：
1 = 0001 
3 = 0011 
4 = 0100 
8 = 1000 
查询的 XOR 值为：
[0,1] = 1 xor 3 = 2 
[1,2] = 3 xor 4 = 7 
[0,3] = 1 xor 3 xor 4 xor 8 = 14 
[3,3] = 8

示例 2：

1 2	输入：arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]] 输出：[8,0,4,4]

提示：

1 <= arr.length <= 3 * 10^4
1 <= arr[i] <= 10^9
1 <= queries.length <= 3 * 10^4
queries[i].length == 2
0 <= queries[i][0] <= queries[i][1] < arr.length

借用前缀和思路的前缀异或

/**
 * @param {number[]} arr
 * @param {number[][]} queries
 * @return {number[]}
 * 前缀异或
 */
var xorQueries = function(arr, queries) {
    // 个数
    const n = arr.length;
    // 存储第i个位置前的数的异或结果
    const xor = new Array(n + 1).fill(0);
    for (let i = 0; i < n; i++) {
        // 按照定义计算
        xor[i + 1] = xor[i] ^ arr[i];
    }
    // 结果数组
    let res = [];
    queries.forEach(item => {
        // 输出，前面的数异或两次后为0，实现两个位置之间的异或
        res.push(xor[item[0]] ^ xor[item[1] + 1]);
    })
    return res;
};

1486. 数组异或操作

给你两个整数，n 和 start 。

数组 nums 定义为：nums[i] = start + 2*i（下标从 0 开始）且 n == nums.length 。

请返回 nums 中所有元素按位异或（XOR）后得到的结果。

示例 1：

输入：n = 5, start = 0
输出：8
解释：数组 nums 为 [0, 2, 4, 6, 8]，其中 (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8 。
     "^" 为按位异或 XOR 运算符。

示例 2：

1
2
3

输入：n = 4, start = 3
输出：8
解释：数组 nums 为 [3, 5, 7, 9]，其中 (3 ^ 5 ^ 7 ^ 9) = 8.

示例 3：

1 2	输入：n = 1, start = 7 输出：7

示例 4：

1 2	输入：n = 10, start = 5 输出：2

提示：

1 <= n <= 1000
0 <= start <= 1000
n == nums.length

模拟法

/**
 * @param {number} n
 * @param {number} start
 * @return {number}
 */
var xorOperation = function(n, start) {
    if (n == 0) return 0;
    let res = 0;
    for (let i = 0; i < n; i++) {
        res ^= start + 2 * i;
    }
    return res;
};

数学方法优化
记 ⊕ 为异或运算，异或运算满足以下性质：

1.x⊕x=0；
2.x⊕y=y⊕x（交换律）；
3.(x⊕y)⊕z=x⊕(y⊕z)（结合律）；
4.x⊕y⊕y=x（自反性）；
5.∀i∈Z，有 4i⊕(4i+1)⊕(4i+2)⊕(4i+3)=0。
在本题中，我们需要计算start⊕(start+2i)⊕(start+4i)⊕⋯⊕(start+2(n−1))。

在本题中，我们需要计算 start⊕(start+2i)⊕(start+4i)⊕⋯⊕(start+2(n−1))。

观察公式可以知道，这些数的奇偶性质相同，因此它们的二进制表示中的最低位或者均为 1，或者均为 0。于是我们可以把参与运算的数的二进制位的最低位提取出来单独处理。当且仅当 start 为奇数，且 n 也为奇数时，结果的二进制位的最低位才为 1。

此时我们可以将公式转化为(s⊕(s+1)⊕(s+2)⊕⋯⊕(s+n−1))×2+e，其中 $s=\lfloor \frac{\textit{start}}{2}]$，e 表示运算结果的最低位。即我们单独处理最低位，而舍去最低位后的数列恰成为一串连续的整数。

这样我们可以描述一个函数sumXor(x)，表示 0⊕1⊕2⊕⋯⊕x。利用异或运算的性质 5，我们可以将计算该函数的复杂度降低到 O(1)，因为以4i 为开头的连续四个整数异或的结果为 0，所以sumXor(x) 可以被表示为：

$$
\text{sumXor}(x)= \begin{cases} x,& x=4k,k\in Z\ (x-1) \oplus x,& x=4k+1,k\in Z\ (x-2) \oplus (x-1) \oplus x,& x=4k+2,k\in Z\ (x-3) \oplus (x-2) \oplus (x-1) \oplus x,& x=4k+3,k\in Z\ \end{cases}
$$

我们可以进一步化简该式：

$$
\text{sumXor}(x)= \begin{cases} x,& x=4k,k\in Z\ 1,& x=4k+1,k\in Z\ x+1,& x=4k+2,k\in Z\ 0,& x=4k+3,k\in Z\ \end{cases}
$$

这样最后的结果即可表示为$$(sumXor(s−1)⊕sumXor(s+n−1))×2+e$$。

/**
 * @param {number} n
 * @param {number} start
 * @return {number}
 */
var xorOperation = function(n, start) {
    let s = start >> 1, e = n & start & 1;
    let ret = sumXor(s - 1) ^ sumXor(s + n - 1);
    return ret << 1 | e;
};

const sumXor = (x) => {
    if (x % 4 === 0) {
        return x;
    }
    if (x % 4 === 1) {
        return 1;
    }
    if (x % 4 === 2) {
        return x + 1;
    }
    return 0;
}

1720. 解码异或后的数组

未知整数数组 arr 由 n 个非负整数组成。

经编码后变为长度为 n - 1 的另一个整数数组 encoded ，其中 encoded[i] = arr[i] XOR arr[i + 1] 。例如，arr = [1,0,2,1] 经编码后得到 encoded = [1,2,3] 。

给你编码后的数组 encoded 和原数组 arr 的第一个元素 first（arr[0]）。

请解码返回原数组 arr 。可以证明答案存在并且是唯一的。

示例 1：

1
2
3

输入：encoded = [1,2,3], first = 1
输出：[1,0,2,1]
解释：若 arr = [1,0,2,1] ，那么 first = 1 且 encoded = [1 XOR 0, 0 XOR 2, 2 XOR 1] = [1,2,3]

示例 2：

1 2	输入：encoded = [6,2,7,3], first = 4 输出：[4,2,0,7,4]

提示：

2 <= n <= 104
encoded.length == n - 1
0 <= encoded[i] <= 105
0 <= first <= 105

位运算

/**
 * @param {number[]} encoded
 * @param {number} first
 * @return {number[]}
 */
var decode = function(encoded, first) {
    let res = [first];
    for (let i = 0; i < encoded.length; i++) {
        res.push(encoded[i] ^ res[i]);
    }
    return res;
};

1734. 解码异或后的排列

给你一个整数数组 perm ，它是前 n 个正整数的排列，且 n 是个奇数。

它被加密成另一个长度为 n - 1 的整数数组 encoded ，满足 encoded[i] = perm[i] XOR perm[i + 1] 。比方说，如果 perm = [1,3,2] ，那么 encoded = [2,1] 。

给你 encoded 数组，请你返回原始数组 perm 。题目保证答案存在且唯一。

示例 1：

1
2
3

输入：encoded = [3,1]
输出：[1,2,3]
解释：如果 perm = [1,2,3] ，那么 encoded = [1 XOR 2,2 XOR 3] = [3,1]

示例 2：

1 2	输入：encoded = [6,5,4,6] 输出：[2,4,1,5,3]

提示：

3 <= n < 105
n 是奇数。
encoded.length == n - 1

利用异或的性质，以及n是个奇数的条件

/**
 * @param {number[]} encoded
 * @return {number[]}
 */
var decode = function(encoded) {
    // 先求出n，是个奇数
    const n = encoded.length + 1;
    // 求出1-n的异或结果
    let xor = 0;
    for (let i = 1; i <= n; i++) {
        xor ^= i;
    }
    let perm = new Array(n).fill(0);
    // 求出第一个数的值
    for (let i = 1; i < n; i += 2) {
        perm[0] ^= encoded[i];
    }
    perm[0] ^= xor;
    // 数组中每个数的值
    for (let i = 1; i < n; i++) {
        perm[i] = perm[i - 1] ^ encoded[i - 1];
    }
    return perm;
};