hxy的博客

Mia san Mia!

0%

排序算法刷题

发表于 更新于 分类于 Valine：

按照算法和数据结构进行分类，一起来刷题，用于自己在面试前查漏补缺。我的意向岗位是前端，选择用javascript来刷题，优点是动态语言，语法简单，缺点是遇见复杂数据结构会出现较难的写法，如堆、并查集，每题对应leetcode的题号。本篇是排序算法

专题部分

排序算法

75. 颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，**原地**对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

示例 1：

1
2
输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

示例 2：

1
2
输入：nums = [2,0,1]
输出：[0,1,2]

示例 3：

1
2
输入：nums = [0]
输出：[0]

示例 4：

1
2
输入：nums = [1]
输出：[1]

提示：

  • n == nums.length
  • 1 <= n <= 300
  • nums[i] 为 0、1 或 2

进阶：

  • 你可以不使用代码库中的排序函数来解决这道题吗？
  • 你能想出一个仅使用常数空间的一趟扫描算法吗？

利用快速排序的思想，用双指针控制0和2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @param {number[]} nums
 * @return {void} Do not return anything, modify nums in-place instead.
 */
var sortColors = function(nums) {
    let left = -1, right = nums.length;
    // 当前位置
    let i = 0;
    // 下标如果遇到 right，说明已经排序完成
    while (i < right) {
        // 遇到0，与左指针交换，位置前进一步
        if (nums[i] === 0) {
            swap(nums, i++, ++left);
        } else if (nums[i] == 1) {
            // 遇到1，位置前进一步
            i++;
        } else {
            // 遇到2，与右指针交换，位置不变
            swap(nums, i, --right);
        }
    }
};
function swap(array, left, right) {
    let temp = array[right];
    array[right] = array[left];
    array[left] = temp;
}

148. 排序链表

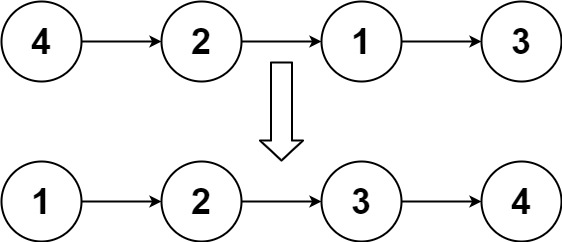
给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

进阶：

  • 你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

示例 1：

img

1
2
输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

1
2
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

1
2
输入：head = []
输出：[]

提示：

  • 链表中节点的数目在范围 [0, 5 * 104] 内
  • -105 <= Node.val <= 105

归并排序法，自上而下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 * 归并排序法，自上而下
 */
var sortList = function(head) {
    // 从头节点到尾节点
    return toSortList(head, null);
};

// 归并两个序列
function merge (head1, head2) {
    const dummyHead = new ListNode(0);
    let temp = dummyHead, temp1 = head1, temp2 = head2;
    while (temp1 !== null && temp2 !== null) {
        if (temp1.val <= temp2.val) {
            temp.next = temp1;
            temp1 = temp1.next;
        } else {
            temp.next = temp2;
            temp2 = temp2.next;
        }
        temp = temp.next;
    }
    // 连接剩余节点
    if (temp1 !== null) {
        temp.next = temp1;
    } else if (temp2 !== null) {
        temp.next = temp2;
    }
    // 返回节点
    return dummyHead.next;
};

// 将两个节点之间排好序
function toSortList (head, tail) {
    // 头指针为空，返回空指针
    if (head === null) {
        return head;
    }
    if (head.next === tail) {
        head.next = null;
        return head;
    }
    // 快慢指针找中点
    let slow = head, fast = head;
    while (fast !== tail) {
        slow = slow.next;
        fast = fast.next;
        if (fast !== tail) {
            fast = fast.next;
        }
    }
    const mid = slow;
    // 返回合并后的节点
    return merge(toSortList(head, mid), toSortList(mid, tail));
};

归并排序法，自下而上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 * 归并排序法，自下而上
 */
var sortList = function(head) {
    // 归并排序只有一个数据或者没有数据
    if (!head || !head.next) return head;
    // 找到中间点
    let slow = head, fast = head.next;
    // 快慢双指针找中点
    while (fast && fast.next) {
        fast = fast.next.next;
        slow = slow.next;
    }
    // 拆成两组链表，递归调用
    let mid = slow.next;
    slow.next = null;
    // 递归调用得到两个排序好的链表
    let left = sortList(head), right = sortList(mid);
    let h = new ListNode();
    let res = h;
    // 进行链表的合并
    while (left && right) {
        if (left.val < right.val) {
            h.next = left;
            left = left.next
        } else {
            h.next = right;
            right = right.next
        }
        h = h.next;
    }
    // 剩下未排好的节点
    h.next = left ? left : right;
    return res.next;
};

215. 数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:

1
2
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例 2:

1
2
输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明:

你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

方法一，直接用库函数 时间复杂度：O(nlogn)，空间复杂度：O(logn)

1
2
3
4
var findKthLargest = function(nums, k) {
    nums.sort((a, b) => b - a);
    return nums[k - 1];
};

方法二，构造k个元素的小顶堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function(nums, k) {
    // 从 nums 中取出前 k 个数，构建一个小顶堆
    buildHeap(nums, k);
    
    // 从 k 位开始遍历数组
    for(let i = k; i < nums.length; i++) {
        if(nums[0] < nums[i]) {
            // 替换并堆化
            nums[0] = nums[i];
            heapify(nums, k, 0);
        }
    }
    
    // 返回堆顶元素
    return nums[0];
};

// 原地建堆，从后往前，自上而下式建小顶堆
let buildHeap = (arr, k) => {
    if(k === 1) return;
    // 从最后一个非叶子节点开始，自上而下式堆化
    for(let i = Math.floor((k - 1) / 2); i >= 0; i--) {
        heapify(arr, k, i);
    }
}

// 堆化
let heapify = (arr, k, i) => {
    // 自上而下式堆化
    while(true) {
        let minIndex = i;
        // 比较和左节点
        if(2 * i + 1 < k && arr[2 * i + 1] < arr[i]) {
            minIndex = 2 * i + 1;
        }
        
        // 比较和右节点
        if(2 * i + 2 < k && arr[2 * i + 2] < arr[minIndex]) {
            minIndex = 2 * i + 2;
        }
        if (minIndex !== i) {
            // 交换和子节点种较小的那个
            swap(arr, i, minIndex);
            i = minIndex;
        } else {
            // 当前节点比左右节点都小，当前位置不用下沉
            break;
        }
    }
}

// 交换
let swap = (arr, i , j) => {
    let temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

方法三：快速排序 时间复杂度：平均时间复杂度O(n)，最坏情况时间复杂度为O(n2)，空间复杂度：O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/**
 * 在数组 nums 的子区间 [left, right] 执行 partition 操作，返回 nums[left] 排序以后应该在的位置
 * 在遍历过程中保持循环不变量的语义
 * 1、[left + 1, j] < nums[left]
 * 2、(j, i] >= nums[left]
 *
 * @param nums
 * @param left
 * @param right
 * @return
 */
function partition(nums, left, right) {
    let pivot = nums[left];
    let j = left;
    for (let i = left + 1; i <= right; i++) {
        if (nums[i] < pivot) {
            // 小于 pivot 的元素都被交换到前面
            j++;
            swap(nums, i, j);
        }
    }
     // 在之前遍历的过程中，满足 [left + 1, j] < pivot，并且 (j, i] >= pivot
     swap(nums, j, left);
     // 交换以后 [left, j - 1] < pivot, nums[j] = pivot, [j + 1, right] >= pivot
     return j;
};

function swap(nums, i, j) {
    let temp = nums[i];
    nums[i] = nums[j];
    nums[j] = temp;
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function(nums, k) {
    let len = nums.length;
    let left = 0;
    let right = len - 1;

    // 转换一下，第 k 大元素的索引是 len - k
    let target = len - k;

    while(true) {
        let index = partition(nums, left, right);
        if (index == target) {
            return nums[target];
        } else if (index < target) {
            left = index + 1;
        } else {
            right = index - 1;
        }
    }
};

347. 前 K 个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

1
2
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

1
2
输入: nums = [1], k = 1
输出: [1]

提示：

  • 1 <= nums.length <= 105
  • k 的取值范围是 [1, 数组中不相同的元素的个数]
  • 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

进阶：你所设计算法的时间复杂度 必须 优于 O(n log n) ，其中 n 是数组大小。

无脑排序时间复杂度 O(n log n)

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    let count = new Map();
    for (let num of nums) {
        count.set(num, (count.get(num) || 0) + 1);
    }
    return Array.from(count).sort((a, b) => b[1] - a[1]).slice(0, k).map(item => item[0]);
};

桶排序

首先使用哈希表统计频率，统计完成后，创建一个数组，将频率作为数组下标，对于出现频率不同的数字集合，存入对应的数组下标即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    let map = new Map();
    nums.map((num) => {
        if(map.has(num))
            map.set(num, map.get(num) + 1);
        else
            map.set(num, 1);
    })
    
    // 如果元素数量小于等于 k
    if(map.size <= k) {
        return [...map.keys()];
    }
    
    return bucketSort(map, k);
};

// 桶排序
function bucketSort (map, k) {
    let arr = [], res = [];
    map.forEach((value, key) => {
        // 利用映射关系（出现频率作为下标）将数据分配到各个桶中
        if(!arr[value]) {
            arr[value] = [key];
        } else {
            arr[value].push(key);
        }
    })
    // 倒序遍历获取出现频率最大的前k个数
    for(let i = arr.length - 1; i >= 0 && res.length < k; i--){
        if(arr[i]) {
            res.push(...arr[i]);
        }
	}
	return res;
}

堆排序
思路与算法

首先遍历整个数组，并使用哈希表记录每个数字出现的次数，并形成一个「出现次数数组」。找出原数组的前 kk个高频元素，就相当于找出「出现次数数组」的前 k 大的值。

最简单的做法是给「出现次数数组」排序。但由于可能有 O(N) 个不同的出现次数（其中 NN 为原数组长度），故总的算法复杂度会达O(NlogN)，不满足题目的要求。

在这里，我们可以利用堆的思想：建立一个小顶堆，然后遍历「出现次数数组」：

如果堆的元素个数小于 k，就可以直接插入堆中。
如果堆的元素个数等于 k，则检查堆顶与当前出现次数的大小。如果堆顶更大，说明至少有 k 个数字的出现次数比当前值大，故舍弃当前值；否则，就弹出堆顶，并将当前值插入堆中。
遍历完成后，堆中的元素就代表了「出现次数数组」中前 k 大的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    let map = new Map(), heap = [, ];
    nums.map((num) => {
        if(map.has(num))
            map.set(num, map.get(num) + 1);
        else
            map.set(num, 1);
    })
    
    // 如果元素数量小于等于 k
    if(map.size <= k) {
        return [...map.keys()];
    }
    
    // 如果元素数量大于 k，遍历map，构建小顶堆
    let i = 0;
    map.forEach((value, key) => {
        if(i < k) {
            // 取前k个建堆, 插入堆
            heap.push(key);
            // 原地建立前 k 堆
            if(i === k - 1) buildHeap(heap, map, k);
        } else if(map.get(heap[1]) < value) {
            // 替换并堆化
            heap[1] = key;
            // 自上而下式堆化第一个元素
            heapify(heap, map, k, 1);
        }
        i++;
    })
    // 删除heap中第一个元素
    heap.shift();
    return heap;
};

// 原地建堆，从后往前，自上而下式建小顶堆
function buildHeap (heap, map, k) {
    if(k === 1) return;
    // 从最后一个非叶子节点开始，自上而下式堆化
    for (let i = Math.floor(k / 2); i >= 1 ; i--) {
        heapify(heap, map, k, i);
    }
}

// 堆化
function heapify (heap, map, k, i) {
    // 自上而下式堆化
    while(true) {
        let minIndex = i;
        if(2 * i <= k && map.get(heap[2 * i]) < map.get(heap[i])) {
            minIndex = 2 * i;
        }
        if(2 * i + 1 <= k && map.get(heap[2 * i + 1]) < map.get(heap[minIndex])) {
            minIndex = 2 * i + 1;
        }
        if(minIndex !== i) {
            swap(heap, i, minIndex);
            i = minIndex;
        } else {
            break;
        }
    }
}

// 交换
function swap (arr, i , j) {
    let temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
-------------本文结束感谢您的阅读-------------

欢迎关注我的其它发布渠道