按照算法和数据结构进行分类,一起来刷题,用于自己在面试前查漏补缺。我的意向岗位是前端,选择用javascript来刷题,优点是动态语言,语法简单,缺点是遇见复杂数据结构会出现较难的写法,如堆、并查集,每题对应leetcode的题号。本篇是剑指offer部分
剑指offer 找出数组中重复的数字。
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
限制:
2 <= n <= 100000
解法一
哈希表,时间复杂度为O(N),空间复杂度为O(N)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 var findRepeatNumber = function (nums ) let hash = new Set (); for (let i = 0 ; i < nums.length; i++){ if (hash.has(nums[i])){ return nums[i]; } else { hash.add(nums[i]); } } return null ; };
解法二
置换,时间复杂度为O(N),空间复杂度为O(1)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 var findRepeatNumber = function (nums ) for (let i = 0 ; i < nums.length; i++) { let cur = nums[i]; if (cur !== i) { if (cur !== nums[cur]) { let temp = nums[cur]; nums[cur] = cur; cur = temp; } else { return cur; } } } };
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:
[
给定 target = 5,返回 true。
给定 target = 20,返回 false。
双指针,时间复杂度为O(m+n)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 var findNumberIn2DArray = function (matrix, target ) if (matrix === null || matrix.length === 0 || matrix[0 ].length === 0 ) return false ; let lenX = matrix.length; let lenY = matrix[0 ].length; let x = 0 , y = lenY - 1 ; while (x < lenX && y >= 0 ){ if (matrix[x][y] === target){ return true ; } else if (matrix[x][y] > target){ y--; } else { x++; } } return false ; };
请实现一个函数,把字符串 s 中的每个空格替换成”%20”。
示例 1:
输入:s = “We are happy.”
限制:
0 <= s 的长度 <= 10000
正则
1 2 3 4 5 6 7 8 var replaceSpace = function (s ) return s.replace(/\s/g , "%20" ) };
库函数
1 2 3 4 5 6 7 8 var replaceSpace = function (s ) return s.split(' ' ).join('%20' ) };
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
示例 1:
1 2 输入:head = [1,3,2] 输出:[2,3,1]
限制:
无需翻转链表
1 2 3 4 5 6 7 8 9 10 var reversePrint = function (head ) let arr = []; while (head !== null ){ arr.unshift(head.val); head = head.next; } return arr; };
翻转链表,额外空间降为0
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var reversePrint = function (head ) if (!head) return []; let pre = head, cur = head.next; while (cur !== null ) { pre.next = cur.next; cur.next = head; head = cur; cur = pre.next; } let res = []; cur = head; while (cur) { res.push(cur.val); cur = cur.next; } return res; };
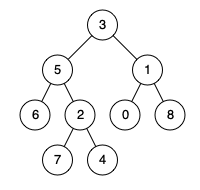
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如,给出
1 2 前序遍历 preorder = [3,9,20,15,7] 中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
限制:
直接递归划分子前序遍历和中序遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var buildTree = function (preorder, inorder ) if (preorder.length <= 0 ) return null ; let node = new TreeNode(preorder[0 ]); let i = inorder.indexOf(preorder[0 ]); node.left = buildTree(preorder.slice(1 , i + 1 ), inorder.slice(0 , i)); node.right = buildTree(preorder.slice(i + 1 , preorder.length), inorder.slice(i + 1 , inorder.length)); return node; };
牺牲空间优化速度,保存每个子节点 在中序遍历中的位置
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 var buildTree = function (preorder, inorder ) if (preorder.length === 0 ) return null ; const map = new Map (); const len = inorder.length; for (let i = 0 ; i < len; i++) { map.set(inorder[i], i); } function tree (pre, inor, pre_start, pre_end, inor_start, inor_end ) const root_val = pre[pre_start]; const root = new TreeNode(root_val); const inor_root_index = map.get(root_val); const lsonLen = inor_root_index - inor_start; const rsonLen = inor_end - inor_root_index; if (lsonLen > 0 ) { root.left = tree(pre, inor, pre_start + 1 , pre_start + 1 + lsonLen, inor_start, inor_root_index - 1 ); } if (rsonLen > 0 ) { root.right = tree(pre, inor, pre_start + 1 + lsonLen, pre_end, inor_root_index + 1 , inor_end); } return root; } return tree(preorder, inorder, 0 , len - 1 , 0 , len - 1 ); };
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开头的元素boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你只能使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
进阶:
你能否实现每个操作均摊时间复杂度为 O(1) 的队列?换句话说,执行 n 个操作的总时间复杂度为 O(n) ,即使其中一个操作可能花费较长时间。
示例:
1 2 3 4 5 6 7 8 9 10 11 12 13 输入: ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出: [null, null, null, 1, 1, false] 解释: MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false
提示:
1 <= x <= 9最多调用 100 次 push、pop、peek 和 empty
假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)
使用第一个栈作为入栈,第二个栈作为出栈
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 var MyQueue = function ( this .stack1 = []; this .stack2 = []; }; MyQueue.prototype.push = function (x ) this .stack1.push(x); }; MyQueue.prototype.pop = function ( if (this .stack2.length) { return this .stack2.pop(); } else { while (this .stack1.length) { this .stack2.push(this .stack1.pop()); } return this .stack2.pop(); } }; MyQueue.prototype.peek = function ( if (this .stack2.length) { return this .stack2[this .stack2.length - 1 ]; } else { while (this .stack1.length) { this .stack2.push(this .stack1.pop()); } return this .stack2[this .stack2.length - 1 ]; } }; MyQueue.prototype.empty = function ( if (this .stack1.length == 0 && this .stack2.length == 0 ) { return true ; } return false ; };
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
1 2 F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
示例 2:
提示:
动态规划已经优化好了空间
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 var fib = function (N ) if (N < 2 ) return N; let dp0 = 0 , dp1 = 1 ; for (let i = 2 ; i <= N; i++) { let temp = dp0 + dp1; dp0 = dp1; dp1 = temp; } return dp1 % 1000000007 ; };
通项公式
1 2 3 4 5 6 7 8 9 10 var fib = function (N ) const sqrt5 = Math .sqrt(5 ); const fibN = Math .pow((1 + sqrt5) / 2 , N) - Math .pow((1 - sqrt5) / 2 , N); return Math .round(fibN / sqrt5); };
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
注意数组中可能存在重复的元素。
示例 1:
示例 2:
说明:
二分查找法(这里考虑了会重复的情况)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 var findMin = function (nums ) let n = nums.length; if (n === 0 ) return 0 ; let left = 0 , right = n - 1 ; while (left < right) { let mid = left + ((right - left) >>> 1 ); if (nums[mid] < nums[right]) { right = mid; } else if (nums[mid] > nums[right]) { left = mid + 1 ; } else if (nums[mid] === nums[right]) { if (nums[left] > nums[mid]) { right = mid; } else if (nums[left] < nums[mid]) { right = left; } else { right--; } } } return nums[left]; };
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[[“a”,”b “,”c”,”e”],f “,”c “,”s”],e “,”e”]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
1 2 输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true
示例 2:
1 2 输入:board = [["a","b"],["c","d"]], word = "abcd" 输出:false
提示:
1 <= board.length <= 2001 <= board[i].length <= 200
回溯法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 var exist = function (board, word ) let row = board.length; let col = board[0 ].length; function dfs (i, j, board, word, index ) if (i < 0 || i >= row || j < 0 || j > col || board[i][j] !== word[index]) return false ; if (index === word.length - 1 ) return true ; let tmp = board[i][j]; board[i][j] = '-' ; let res = dfs(i - 1 , j, board, word, index + 1 ) || dfs(i + 1 , j, board, word, index + 1 ) || dfs(i, j - 1 , board, word, index + 1 ) || dfs(i, j + 1 , board, word, index + 1 ); board[i][j] = tmp; return res; } for (let i = 0 ; i < row; i++){ for (let j = 0 ; j < col; j++){ if (dfs(i, j, board, word, 0 )) return true ; } } return false ; };
地上有一个m行n列的方格,从坐标 [0, 0] 到坐标 [m - 1, n - 1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
1 2 输入:m = 2, n = 3, k = 1 输出:3
示例 2:
1 2 输入:m = 3, n = 1, k = 0 输出:1
提示:
1 <= n,m <= 1000 <= k <= 20
思路是如果一个数从上方和左方无法访问,从下方和右方也无法访问
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 var movingCount = function (m, n, k ) if (!k) return 1 ; let vis = new Array (m); let count = 0 ; var countSum = function (n ) let sum = 0 ; while (n) { sum += n % 10 ; n = Math .floor(n / 10 ); } return sum; } for (let i = 0 ; i < m; i++) { vis[i] = new Array (n); for (let j = 0 ; j < n; j++) { let sum = countSum(i) + countSum(j); if (i === 0 && j === 0 ) { vis[i][j] = sum <= k; } else if (i === 0 ) { vis[i][j] = vis[i][j - 1 ] && (sum <= k); } else if (j === 0 ) { vis[i][j] = vis[i - 1 ][j] && (sum <= k); } else { vis[i][j] = (vis[i - 1 ][j] || vis[i][j - 1 ]) && (sum <= k); } if (vis[i][j]) count++; } } return count; };
给定一个正整数 n ,将其拆分为至少 两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
1 2 3 输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
1 2 3 输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
尽可能拆分更多的3,多1的话拆分成2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 var cuttingRope = function (n ) if (n < 4 ) return n - 1 ; let r = Math .floor(n / 3 ); switch (n % 3 ) { case 0 : return Math .pow(3 , r) % 1000000007 ; case 1 : return 4 * Math .pow(3 , r - 1 ) % 1000000007 ; case 2 : return 2 * Math .pow(3 , r) % 1000000007 ; } }
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量 )。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码 记法来表示有符号整数。因此,在上面的 示例 3 中,输入表示有符号整数 -3。
示例 1:
1 2 3 输入:00000000000000000000000000001011 输出:3 解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
1 2 3 输入:00000000000000000000000010000000 输出:1 解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
1 2 3 输入:11111111111111111111111111111101 输出:31 解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
进阶 :
位运算通过n &= n - 1消去末尾的1
1 2 3 4 5 6 7 8 9 10 11 12 var hammingWeight = function (n ) let number = 0 ; while (n) { number++; n &= n - 1 ; } return number; };
实现 pow(x , n ) ,即计算 x 的 n 次幂函数。不得使用库函数,同时不需要考虑大数问题。
示例 1:
1 2 输入:x = 2.00000, n = 10 输出:1024.00000
示例 2:
1 2 输入:x = 2.10000, n = 3 输出:9.26100
示例 3:
1 2 3 输入:x = 2.00000, n = -2 输出:0.25000 解释:2^(-2) = (1/2)^2 = 1/4 = 0.25
提示:
-100.0 < x < 100.0-231 <= n <= 231-1-104 <= xn <= 104
先把问题转换求幂为正数的情况,再通过幂的位运算求出结果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var myPow = function (x, n ) if (x === 0 || x === 1 ) return x; x = n >= 0 ? x: 1 / x; if (n !== -2147483648 ) { n = n >= 0 ? n: -n; } else { n = 2147483648 / 2 ; x = x * x; } let res = 1 ; while (n) { if (n & 1 ) res *= x; x *= x; n >>= 1 ; } return res; };
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数 999。
示例 1:
1 2 输入: n = 1 输出: [1,2,3,4,5,6,7,8,9]
说明:
考虑大数,使用字符串进行操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 var printNumbers = function (n ) if (n <= 0 ) return [] let current = [1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ]; let next = []; let result = [...current]; while (n > 1 ) { for (let num of current) { for (let i = 0 ; i < 10 ; i++) { const newNum = parseInt (String (num) + String (i)); next.push(newNum); } } result = [...result, ...next]; current = next; next = []; n--; } return result; }
给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
返回删除后的链表的头节点。
注意: 此题对比原题有改动
示例 1:
1 2 3 输入: head = [4,5,1,9], val = 5 输出: [4,1,9] 解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
示例 2:
1 2 3 输入: head = [4,5,1,9], val = 1 输出: [4,5,9] 解释: 给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.
说明:
题目保证链表中节点的值互不相同
若使用 C 或 C++ 语言,你不需要 free 或 delete 被删除的节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 var deleteNode = function (head, val ) if (!head) return null ; let dummy = new ListNode(0 ); dummy.next = head; let cur = dummy; while (cur.next) { if (cur.next.val === val) { cur.next = cur.next.next; break ; } cur = cur.next; } return dummy.next; };
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
1 2 3 输入:s = "aa" p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
1 2 3 输入:s = "aa" p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
1 2 3 输入:s = "ab" p = ".*" 输出:true 解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
1 2 3 输入:s = "aab" p = "c*a*b" 输出:true 解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
1 2 输入:s = "mississippi" p = "mis*is*p*." 输出:false
提示:
0 <= s.length <= 200 <= p.length <= 30s 可能为空,且只包含从 a-z 的小写字母。p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。保证每次出现字符 * 时,前面都匹配到有效的字符
没什么好说的,动态规划走起
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 var isMatch = function (s, p ) if (!p) return !s; let m = s.length, n = p.length; let dp = Array .from(Array (m + 1 ), () => Array (n + 1 ).fill(false )); dp[0 ][0 ] = true ; for (let j = 2 ; j <= n; j++) { if (p[j - 1 ] === '*' ){ dp[0 ][j] = dp[0 ][j - 2 ]; } } for (let i = 1 ; i <= m; i++) { for (let j = 1 ; j <= n; j++) { if (s[i - 1 ] === p[j - 1 ] || p[j - 1 ] === '.' ) { dp[i][j] = dp[i - 1 ][j - 1 ]; } else if (j >= 2 && p[j - 1 ] === '*' ) { if ((s[i - 1 ] === p[j - 2 ] || p[j - 2 ] === '.' )) { dp[i][j] = dp[i][j - 1 ] || dp[i - 1 ][j] || dp[i][j - 2 ]; } else { dp[i][j] = dp[i][j - 2 ]; } } } } return dp[m][n]; };
优化一下空间,这个空间压缩稍微费点事,要考虑原本默认为false的所有情况,相对有点繁琐
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 var isMatch = function (s, p ) if (!p) return !s; let m = s.length, n = p.length; let dp = new Array (n + 1 ).fill(false ); dp[0 ] = true ; for (let j = 2 ; j <= n; j++) { if (p[j - 1 ] === '*' ){ dp[j] = dp[j - 2 ]; } } dp[0 ] = false ; for (let i = 1 ; i <= m; i++) { let pre = i === 1 ? true : false ; for (let j = 1 ; j <= n; j++) { let temp = dp[j]; if (s[i - 1 ] === p[j - 1 ] || p[j - 1 ] === '.' ) { dp[j] = pre; } else if (j >= 2 && p[j - 1 ] === '*' ) { if ((s[i - 1 ] === p[j - 2 ] || p[j - 2 ] === '.' )) { dp[j] = dp[j - 1 ] || dp[j] || dp[j - 2 ]; } else { dp[j] = dp[j - 2 ]; } } else { dp[j] = false ; } pre = temp; } } return dp[n]; };
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串”+100”、”5e2”、”-123”、”3.1416”、”-1E-16”、”0123”都表示数值,但”12e”、”1a3.14”、”1.2.3”、”+-5”及”12e+5.4”都不是。
利用js内置的isNaN函数
1 2 3 4 5 6 7 8 9 var isNumber = function (s ) s = s.trim(); if (!s) return false ; return !isNaN (s); };
采用正则表达式,这个很直观,就是要耐心写
1 2 3 4 5 6 7 8 var isNumber = function (s ) return /^[+-]?\d*(\.\d+)?([eE][+-]?\d+)?$/ .test(s.trim()); };
有限自动状态机,这个真的难写,自己想都要想很久,更别说写了,重在理解状态机的概念,比如promise本质就是个状态机
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 var isNumber = function (s ) let state = 0 , finals = [0 , 0 , 0 , 1 , 0 , 1 , 1 , 0 , 1 ], transfer = [[ 0 , 1 , 6 , 2 ,-1 ,-1 ], [-1 ,-1 , 6 , 2 ,-1 ,-1 ], [-1 ,-1 , 3 ,-1 ,-1 ,-1 ], [ 8 ,-1 , 3 ,-1 , 4 ,-1 ], [-1 , 7 , 5 ,-1 ,-1 ,-1 ], [ 8 ,-1 , 5 ,-1 ,-1 ,-1 ], [ 8 ,-1 , 6 , 3 , 4 ,-1 ], [-1 ,-1 , 5 ,-1 ,-1 ,-1 ], [ 8 ,-1 ,-1 ,-1 ,-1 ,-1 ]], make = (c ) => { switch (c) { case " " : return 0 ; case "+" : case "-" : return 1 ; case "." : return 3 ; case "e" : case "E" :return 4 ; default : let code = c.charCodeAt(); if (code >= 48 && code <= 57 ) { return 2 ; } else { return 5 ; } } }; for (let i = 0 ; i < s.length; i++) { state = transfer[state][make(s[i])]; if (state < 0 ) return false ; } return finals[state]; };
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。
示例:
1 2 3 输入:nums = [1,2,3,4] 输出:[1,3,2,4] 注:[3,1,2,4] 也是正确的答案之一。
提示:
0 <= nums.length <= 500001 <= nums[i] <= 10000
额外空间O(1),时间O(N)需要使用双指针
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var exchange = function (nums ) if (!nums.length) return nums; let left = 0 , right = nums.length - 1 ; while (left < right) { if (nums[left] & 1 ) { left++; } else { [nums[left], nums[right]] = [nums[right], nums[left]]; right--; } } return nums; };
输入一个链表,输出该链表中倒数第k个节点。为了符合大多数人的习惯,本题从1开始计数,即链表的尾节点是倒数第1个节点。
例如,一个链表有 6 个节点,从头节点开始,它们的值依次是 1、2、3、4、5、6。这个链表的倒数第 3 个节点是值为 4 的节点。
示例:
1 2 3 给定一个链表: 1->2->3->4->5, 和 k = 2. 返回链表 4->5.
采用双指针解决
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 var getKthFromEnd = function (head, k ) if (head === null ) { return head; } let fast = head, slow = head; for (let i = 0 ; i < k; i++) { if (fast === null ) return null ; fast = fast.next; } while (fast !== null ) { fast = fast.next; slow = slow.next; } return slow; };
反转一个单链表。
示例:
1 2 输入: 1->2->3->4->5->NULL 输出: 5->4->3->2->1->NULL
进阶:
迭代法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var reverseList = function (head ) if (head === null ) return null ; let pre = head, cur = head.next; while (cur !== null ){ pre.next = cur.next; cur.next = head; head = cur; cur = pre.next; } return head; };
递归方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var reverseList = function (head ) if (head === null || head.next === null ) { return head; } const newHead = reverseList(head.next); head.next.next = head; head.next = null ; return newHead; };
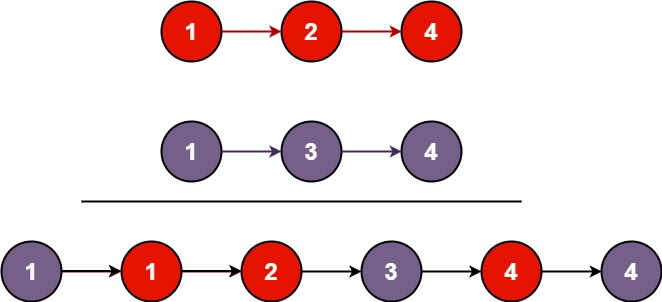
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
1 2 输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]
示例 2:
1 2 输入:l1 = [], l2 = [] 输出:[]
示例 3:
1 2 输入:l1 = [], l2 = [0] 输出:[0]
双指针,O(m+n)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 var mergeTwoLists = function (l1, l2 ) let dummy = new ListNode(0 ); let cur = dummy; while (l1 !== null && l2 !== null ) { if (l1.val <= l2.val) { cur.next = l1; l1 = l1.next; } else { cur.next = l2; l2 = l2.next; } cur = cur.next; } cur.next = l1 ? l1 : l2; return dummy.next; };
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 B:
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
1 2 输入:A = [1,2,3], B = [3,1] 输出:false
示例 2:
1 2 输入:A = [3,4,5,1,2], B = [4,1] 输出:true
限制:
递归法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var isSubStructure = function (A, B ) if (A === null || B === null ) return false ; var isSub = function (A, B ) if (B === null ) return true ; if (A === null ) return false ; if (A.val !== B.val) return false ; return isSub(A.left, B.left) && isSub(A.right, B.right); } return isSub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B); };
请完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
1 2 3 4 5 4 / \ 2 7 / \ / \ 1 3 6 9
镜像输出:
1 2 3 4 5 4 / \ 7 2 / \ / \ 9 6 3 1
示例 1:
1 2 输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]
限制:
递归法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 var invertTree = function (root ) if (root == null ){ return root; } const temp = root.left; root.left = root.right; root.right = temp; invertTree(root.left); invertTree(root.right); return root; };
请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。
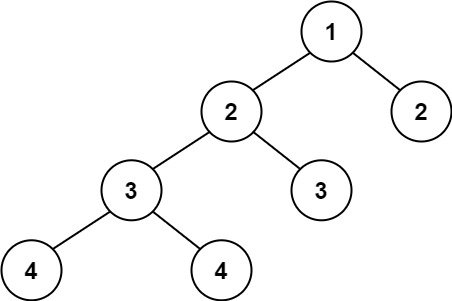
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1 2 3 4 5 1 / \ 2 2 / \ / \ 3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
示例 1:
1 2 输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
1 2 输入:root = [1,2,2,null,3,null,3] 输出:false
限制:
递归法,DFS
1 2 3 4 5 6 7 8 9 var isSymmetric = function (root ) function isSame (left, right ) if (!left && !right) return true ; if (!left || !right) return false ; if (left.val !== right.val) return false ; return isSame(left.left, right.right) && isSame(left.right, right.left); } return isSame(root, root); };
迭代法,BFS
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var isSymmetric = function (root ) let queue = [root, root]; while (queue.length) { let node1 = queue.shift(); let node2 = queue.shift(); if (!node1 && !node2) continue ; if (!node1 || !node2) return false ; if (node1.val !== node2.val) return false ; queue.push(node1.left); queue.push(node2.right); queue.push(node1.right); queue.push(node2.left); } return true ; };
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
示例 1:
1 2 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]
示例 2:
1 2 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出:[1,2,3,4,8,12,11,10,9,5,6,7]
限制:
0 <= matrix.length <= 1000 <= matrix[i].length <= 100
模拟方法,实现模拟螺旋的过程
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 var spiralOrder = function (matrix ) let arr = []; if (matrix === null || matrix.length === 0 ) return arr; let minX = 0 , maxX = matrix.length - 1 ; if (matrix[0 ].length === 0 ) return arr; let minY = 0 , maxY = matrix[0 ].length - 1 ; while (minX <= maxX && minY <= maxY) { if (minX <= maxX && minY <= maxY){ for (let j = minY; j <= maxY; j++) { arr.push(matrix[minX][j]); } minX++; } if (minX <= maxX && minY <= maxY){ for (let i = minX; i <= maxX; i++) { arr.push(matrix[i][maxY]); } maxY--; } if (minX <= maxX && minY <= maxY){ for (let j = maxY; j >= minY; j--) { arr.push(matrix[maxX][j]); } maxX--; } if (minX <= maxX && minY <= maxY){ for (let i = maxX; i >= minX; i--) { arr.push(matrix[i][minY]); } minY++; } } return arr; };
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。
push(x) —— 将元素 x 推入栈中。
示例:
输入:
1 2 ["MinStack","push","push","push","getMin","pop","top","getMin"] [[],[-2],[0],[-3],[],[],[],[]]
输出:
1 [null,null,null,null,-3,null,0,-2]
解释:
1 2 3 4 5 6 7 8 MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> 返回 -3. minStack.pop(); minStack.top(); --> 返回 0. minStack.getMin(); --> 返回 -2.
提示:
pop、top 和 getMin 操作总是在 非空栈 上调用。
最小栈栈顶存储最小的数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 var MinStack = function ( this .stack = []; this .min = []; }; MinStack.prototype.push = function (x ) this .stack.push(x); if (this .min.length === 0 || x <= this .min[this .min.length - 1 ]) this .min.push(x); }; MinStack.prototype.pop = function ( if (this .stack.length === 0 ) { return null ; } else { let temp = this .stack.pop(); if (temp === this .min[this .min.length - 1 ]) { this .min.pop(); } return temp; } }; MinStack.prototype.top = function ( if (this .stack.length === 0 ) return null ; return this .stack[this .stack.length - 1 ]; }; MinStack.prototype.getMin = function ( if (this .min.length === 0 ) return null ; return this .min[this .min.length - 1 ]; };
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
1 2 3 4 5 输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1] 输出:true 解释:我们可以按以下顺序执行: push(1), push(2), push(3), push(4), pop() -> 4, push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
1 2 3 输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2] 输出:false 解释:1 不能在 2 之前弹出。
提示:
0 <= pushed.length == popped.length <= 10000 <= pushed[i], popped[i] < 1000pushed 是 popped 的排列。
模拟栈的实现,检验序列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 var validateStackSequences = function (pushed, popped ) let stack = []; let i = 0 ; for (let num of pushed) { stack.push(num); while (stack.length && stack[stack.length - 1 ] === popped[i]) { stack.pop(); i++; } } return stack.length === 0 ; };
从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
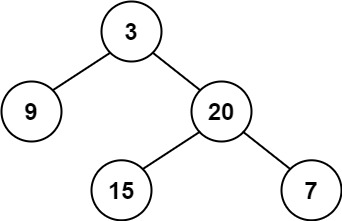
例如:[3,9,20,null,null,15,7],
返回:
提示:
节点总数 <= 1000
总之BFS都是用的队列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 var levelOrder = function (root ) if (!root) return []; let queue = [root]; let result = []; while (queue.length) { let nowNode = queue.shift(); result.push(nowNode.val); nowNode.left && queue.push(nowNode.left); nowNode.right && queue.push(nowNode.right); } return result; };
从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
例如:[3,9,20,null,null,15,7],
返回其层次遍历结果:
1 2 3 4 5 [ [3], [9,20], [15,7] ]
提示:
节点总数 <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 var levelOrder = function (root ) if (root === null ) return []; let queue = [root]; let number = []; let level = 0 ; while (queue.length > 0 ){ number[level] = []; let len = queue.length; while (len--) { let node = queue.shift(); number[level].push(node.val); node.left && queue.push(node.left); node.right && queue.push(node.right); } level++; } return number; };
请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
例如:[3,9,20,null,null,15,7],
返回其层次遍历结果:
1 2 3 4 5 [ [3], [20,9], [15,7] ]
提示:
节点总数 <= 1000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 var levelOrder = function (root ) if (!root) return []; const queue = [root]; const res = []; let level = 0 ; while (queue.length){ res[level] = []; let levelNum = queue.length; while (levelNum--) { const front = queue.shift(); res[level].push(front.val); if (front.left) queue.push(front.left); if (front.right) queue.push(front.right); } if (level % 2 ) { res[level].reverse(); } level++; } return res; };
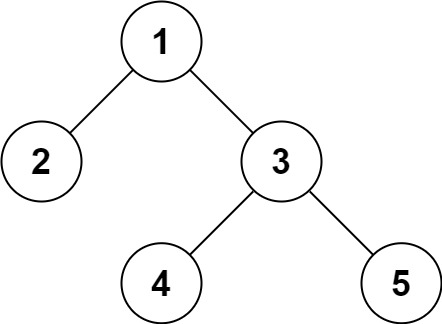
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
示例 1:
1 2 输入: [1,6,3,2,5] 输出: false
示例 2:
1 2 输入: [1,3,2,6,5] 输出: true
提示:
数组长度 <= 1000
利用左子树<根节点<右子树性质,进行递归判断
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var verifyPostorder = function (postorder ) let stack = []; let root = Number .MAX_SAFE_INTEGER; for (let i = postorder.length - 1 ; i >= 0 ; i--){ if (postorder[i] > root) { return false ; } while (stack.length > 0 && postorder[i] < stack[stack.length - 1 ]) { root = stack.pop(); } stack.push(postorder[i]); } return true ; };
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
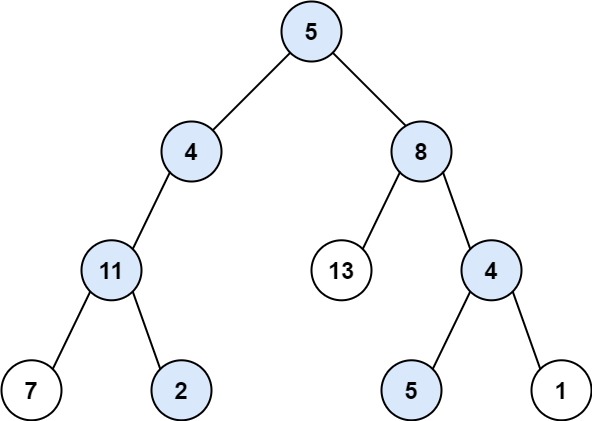
示例 1:
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
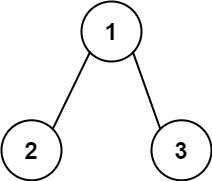
1 2 输入:root = [1,2,3], targetSum = 5 输出:[]
示例 3:
1 2 输入:root = [1,2], targetSum = 0 输出:[]
提示:
树中节点总数在范围 [0, 5000] 内
选择DFS算法保存路径
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 var pathSum = function (root, sum ) let res = []; let path = []; function dfs (root, sum ) if (!root) { return ; } sum -= root.val; path.push(root.val); if (!root.left && !root.right) { if (sum === 0 ) res.push([...path]); } if (root.left) dfs(root.left, sum); if (root.right) dfs(root.right, sum); path.pop(); } dfs(root, sum); return res; };
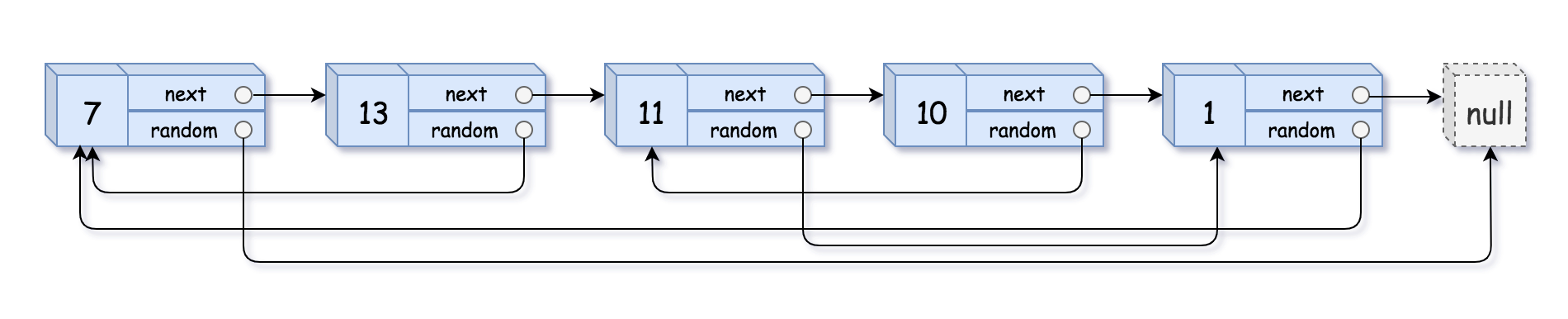
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random –> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random –> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
示例 1:
1 2 输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
1 2 输入:head = [[1,1],[2,1]] 输出:[[1,1],[2,1]]
示例 3:
1 2 输入:head = [[3,null],[3,0],[3,null]] 输出:[[3,null],[3,0],[3,null]]
示例 4:
解释:给定的链表为空(空指针),因此返回 null。
提示:
0 <= n <= 1000
使用哈希表+单向遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 var copyRandomList = function (head ) if (head == null ) return null ; let map = new Map (); let node = head; let newHead = new Node(node.val); let newNode = newHead; map.set(head, newHead); while (node.next) { node = node.next; newNode.next = new Node(node.val); newNode = newNode.next; map.set(node, newNode); } node = head; newNode = newHead; while (node) { newNode.random = map.get(node.random); node = node.next; newNode = newNode.next; } return newHead; };
使用哈希表+递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 let visitedHash = new Map ();var copyRandomList = function (head ) if (head == null ) return null ; if (visitedHash.has(head)) { return visitedHash.get(head); } let node = new Node(head.val); visitedHash.set(head, node); node.next = copyRandomList(head.next); node.random = copyRandomList(head.random); return node; };
先遍历并复制当前节点,再次遍历分成两个完全相同的链表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 var copyRandomList = function (head ) if (head == null ){ return null ; } let head_t = head; while (head_t !== null ){ let tmp = head_t.next; head_t.next = new Node(head_t.val, tmp, null ); head_t = tmp; } head_t = head; while (head_t !== null ){ head_t.next.random = head_t.random ? head_t.random.next : null ; head_t = head_t.next.next; } head_t = head; let result = head_t.next; while (head_t !== null ){ let newOne = head_t.next; head_t.next = newOne.next; newOne.next = newOne.next ? newOne.next.next : null ; head_t = head_t.next; } return result; };
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
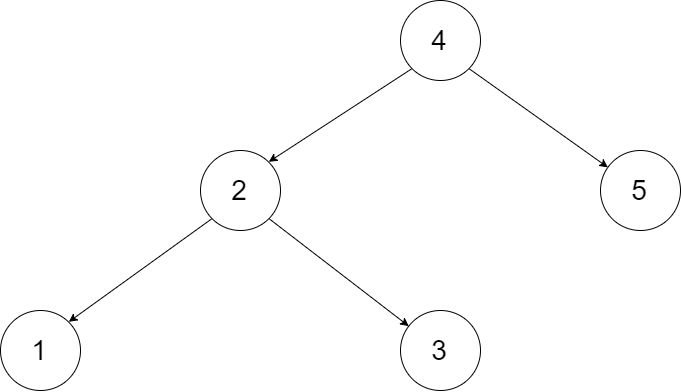
为了让您更好地理解问题,以下面的二叉搜索树为例:
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
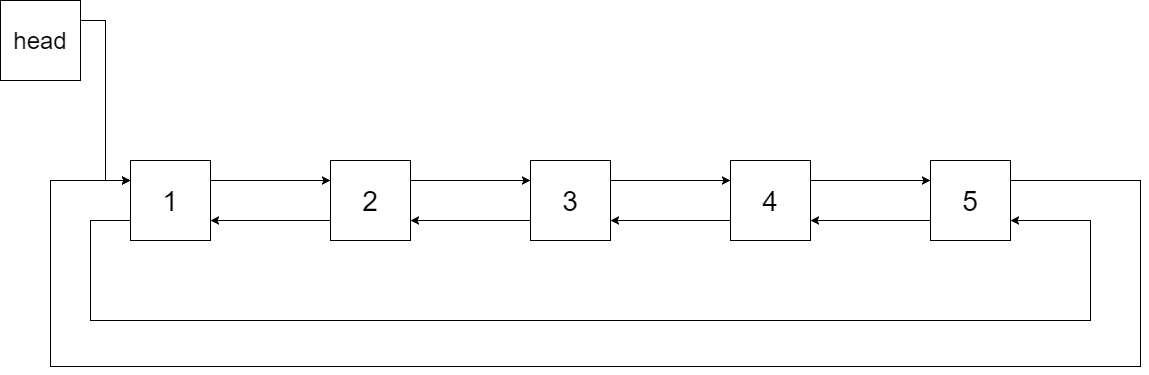
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
利用中序遍历进行迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 var treeToDoublyList = function (root ) if (!root) return root; let head = new TreeNode(0 ); let stack = []; let cur = root; let pre = head; while (cur || stack.length > 0 ) { while (cur) { stack.push(cur); cur = cur.left; } cur = stack.pop(); pre.right = cur; cur.left = pre; pre = cur; cur = cur.right; } pre.right = head.right; head.right.left = pre; return head.right; };
想不出来就用最土的方法,中序遍历将节点存入数组,然后再次遍历数组实现转换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 var treeToDoublyList = function (root ) if (!root) return ; let arr = []; inOrder(root); function inOrder (root ) if (!root) return ; inOrder(root.left); arr.push(root); inOrder(root.right); } for (let i = 0 ; i < arr.length - 1 ; i++) { arr[i].right = arr[i + 1 ]; arr[i + 1 ].left = arr[i]; } len = arr.length; arr[len - 1 ].right = arr[0 ]; arr[0 ].left = arr[len - 1 ]; return arr[0 ]; };
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
提示: 输入输出格式与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
示例 1:
1 2 输入:root = [1,2,3,null,null,4,5] 输出:[1,2,3,null,null,4,5]
示例 2:
示例 3:
示例 4:
1 2 输入:root = [1,2] 输出:[1,2]
提示:
树中结点数在范围 [0, 104] 内
采用,作为分隔符,空元素记为’null’,前序遍历实现序列化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 var rserialize = function (root, str ) if (root === null ) { str += "null," ; return str; } str += root.val + "," ; str = rserialize(root.left, str); str = rserialize(root.right, str); return str; }; var serialize = function (root ) return rserialize(root, "" ); }; var rdeserialize = function (arr ) if (arr[0 ] === "null" ) { arr.shift(); return null ; } let node = new TreeNode(arr.shift()); node.left = rdeserialize(arr); node.right = rdeserialize(arr); return node; }; var deserialize = function (data ) let datalist = data.split("," ); return rdeserialize(datalist); };
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
1 2 输入:s = "abc" 输出:["abc","acb","bac","bca","cab","cba"]
限制:
使用排序后的数组进行带有重复元素的全排列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var permutation = function (s ) let strArr = s.split('' ); strArr.sort(); let res = []; let path = []; let n = strArr.length; let used = new Array (n).fill(false ); function backtrack (arr, path, used, res ) if (path.length === n) res.push([...path].join('' )); for (let i = 0 ; i < n; i++) { if (used[i] || (i > 0 && arr[i] === arr[i - 1 ] && !used[i - 1 ])) continue ; path.push(arr[i]); used[i] = true ; backtrack(arr, path, used, res); path.pop(); used[i] = false ; } } backtrack(strArr, path, used, res); return res; };
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
1 2 输入: [1, 2, 3, 2, 2, 2, 5, 4, 2] 输出: 2
限制:
投票算法,超过一半的数上台投票小于0,下台,当前票上台
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var majorityElement = function (nums ) let vote = 0 ; let x; for (let i = 0 ; i < nums.length; i++) { if (vote === 0 ) { x = nums[i]; } if (nums[i] === x) { vote++; } else { vote--; } } return x; };
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
示例 1:
1 2 输入:arr = [3,2,1], k = 2 输出:[1,2] 或者 [2,1]
示例 2:
1 2 输入:arr = [0,1,2,1], k = 1 输出:[0]
限制:
0 <= k <= arr.length <= 100000 <= arr[i] <= 10000
创建长度为k的大顶堆,当前元素大于堆顶就进行交换
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 var getLeastNumbers = function (arr, k ) if (!k || !arr.length || k > arr.length) { return []; } createHeap(arr, k); for (let i = k; i < arr.length; i++) { if (arr[i] < arr[0 ]) { [arr[i], arr[0 ]] = [arr[0 ], arr[i]]; adjustHeap(arr, 0 , k); } } return arr.slice(0 , k); function createHeap (arr, length ) for (let i = Math .floor(length / 2 ) - 1 ; i >= 0 ; i--) { adjustHeap(arr, i, length); } } function adjustHeap (arr, index, length ) for (let i = 2 * index + 1 ; i < length; i = 2 * i + 1 ) { if (i + 1 < length && arr[i + 1 ] > arr[i]) { i++; } if (arr[index] < arr[i]) { [arr[index], arr[i]] = [arr[i], arr[index]]; index = i; } else { break ; } } } };
快速分割法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 var getLeastNumbers = function (arr, k ) if (k === 0 || arr.length === 0 ) return []; return quickSearch(arr, 0 , arr.length - 1 , k - 1 ); }; function quickSearch (nums, lo, hi, k ) let j = partition(nums, lo, hi); if (j === k) return nums.slice(0 , j + 1 ); return j > k ? quickSearch(nums, lo, j - 1 , k) : quickSearch(nums, j + 1 , hi, k); } function partition (nums, lo, hi ) let v = nums[lo]; let i = lo, j = hi + 1 ; while (true ) { while (++i <= hi && nums[i] < v); while (--j >= lo && nums[j] > v); if (i >= j) break ; let t = nums[j]; nums[j] = nums[i]; nums[i] = t; } nums[lo] = nums[j]; nums[j] = v; return j; }
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例 1:
1 2 3 4 输入: ["MedianFinder","addNum","addNum","findMedian","addNum","findMedian"] [[],[1],[2],[],[3],[]] 输出:[null,null,null,1.50000,null,2.00000]
示例 2:
1 2 3 4 输入: ["MedianFinder","addNum","findMedian","addNum","findMedian"] [[],[2],[],[3],[]] 输出:[null,null,2.00000,null,2.50000]
限制:
最多会对 addNum、findMedian 进行 50000 次调用。
始终维护一个单调序列,使用二分查找法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 var MedianFinder = function ( this .stack = []; }; MedianFinder.prototype.addNum = function (num ) if (this .stack.length === 0 ) { this .stack.push(num); return ; } let left = 0 , right = this .stack.length - 1 ; while (left <= right) { let mid = Math .floor((left + right) / 2 ); if (this .stack[mid] === num) { this .stack.splice(mid, 0 , num); return ; } else if (this .stack[mid] < num) { left = mid + 1 ; } else { right = mid - 1 ; } } this .stack.splice(left, 0 , num); }; MedianFinder.prototype.findMedian = function ( if (this .stack.length === 0 ) { return null ; } let mid = Math .floor((this .stack.length - 1 ) / 2 ); if (this .stack.length % 2 === 1 ) { return this .stack[mid]; } else { return (this .stack[mid] + this .stack[mid + 1 ]) / 2 ; } };
维护一个大根堆(存储较小的一半数)和一个小根堆(存储较大的一半数),实现中位数的计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 var MedianFinder = function ( this .bigHeap = []; this .smallHeap = []; }; MedianFinder.prototype.addNum = function (num ) const bigHeapTop = this .bigHeap[0 ]; const smallHeapTop = this .smallHeap[0 ]; if (this .bigHeap.length === this .smallHeap.length) { if (this .bigHeap.length === 0 ) { this .bigHeap.push(num); } else { if (num <= bigHeapTop) { const isBigHeap = true ; addElementToHeap(this .bigHeap, num, isBigHeap); } else if (num >= smallHeapTop) { const isBigHeap = false ; addElementToHeap(this .smallHeap, num, isBigHeap); } else { const isBigHeap = true ; addElementToHeap(this .bigHeap, num, isBigHeap); } } } else if (this .bigHeap.length > this .smallHeap.length) { if (num <= bigHeapTop) { deleteHeapTop(this .bigHeap, true ); addElementToHeap(this .bigHeap, num, true ); addElementToHeap(this .smallHeap, bigHeapTop, false ); } else if (num >= smallHeapTop) { const isBigHeap = false ; addElementToHeap(this .smallHeap, num, isBigHeap); } else { const isBigHeap = false ; addElementToHeap(this .smallHeap, num, isBigHeap); } } else if (this .bigHeap.length < this .smallHeap.length) { if (num <= bigHeapTop) { const isBigHeap = true ; addElementToHeap(this .bigHeap, num, isBigHeap); } else if (num >= smallHeapTop) { deleteHeapTop(this .smallHeap, false ); addElementToHeap(this .smallHeap, num, false ); addElementToHeap(this .bigHeap, smallHeapTop, true ); } else { const isBigHeap = true ; addElementToHeap(this .bigHeap, num, isBigHeap); } } }; MedianFinder.prototype.findMedian = function ( const bigHeapTop = this .bigHeap[0 ]; const smallHeapTop = this .smallHeap[0 ]; if (this .bigHeap.length === this .smallHeap.length) { if (this .bigHeap.length === 0 ) { return undefined ; } else { return (bigHeapTop + smallHeapTop) / 2 ; } } else if (this .bigHeap.length > this .smallHeap.length) { return bigHeapTop; } else if (this .bigHeap.length < this .smallHeap.length) { return smallHeapTop; } }; function addElementToHeap (arr, num, isBigHeap ) arr.push(num); if (arr.length === 1 ) { return ; } const lastIndex = arr.length - 1 ; let needAdjustParentIndex = Math .floor((lastIndex - 1 ) / 2 ); let lastValidParentIndex = Math .floor(lastIndex / 2 ); while (needAdjustParentIndex >= 0 && needAdjustParentIndex <= lastValidParentIndex) { const oldParentValue = arr[needAdjustParentIndex]; adjustHeap(arr, needAdjustParentIndex, lastIndex, isBigHeap); const changed = oldParentValue !== arr[needAdjustParentIndex]; if (changed) { needAdjustParentIndex = Math .floor((needAdjustParentIndex - 1 ) / 2 ); } else { break ; } } } function deleteHeapTop (arr, isBigHeap ) if (arr.length === 0 ) { return ; } if (arr.length <= 2 ) { arr.shift(); return ; } swap(arr, 0 , arr.length - 1 ); arr.pop(); adjustHeap(arr, 0 , arr.length - 1 , isBigHeap); } function adjustHeap (arr, parentIndex, lastIndex, isBigHeap ) if (typeof isBigHeap !== 'boolean' ) { throw new Error ('miss isBigHeap param for adjustHeap()' ); } if (lastIndex >= 1 && parentIndex <= Math .floor(lastIndex / 2 )) { const leftChildIndex = parentIndex * 2 + 1 ; const rightChildIndex = leftChildIndex + 1 ; if (isBigHeap) { let maxValueIndex = parentIndex; if (leftChildIndex <= lastIndex && arr[leftChildIndex] > arr[maxValueIndex]) { maxValueIndex = leftChildIndex; } if (rightChildIndex <= lastIndex && arr[rightChildIndex] > arr[maxValueIndex]) { maxValueIndex = rightChildIndex; } if (maxValueIndex !== parentIndex) { swap(arr, parentIndex, maxValueIndex); adjustHeap(arr, maxValueIndex, lastIndex, isBigHeap); } } else { let minValueInex = parentIndex; if (leftChildIndex <= lastIndex && arr[leftChildIndex] < arr[minValueInex]) { minValueInex = leftChildIndex; } if (rightChildIndex <= lastIndex && arr[rightChildIndex] < arr[minValueInex]) { minValueInex = rightChildIndex; } if (minValueInex !== parentIndex) { swap(arr, parentIndex, minValueInex); adjustHeap(arr, minValueInex, lastIndex, isBigHeap); } } } } function swap (arr, i, j ) const temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例 1:
1 2 输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。示例 2:
示例 3:
示例 4:
示例 5:
1 2 输入:nums = [-100000] 输出:-100000
提示:
1 2 1 <= nums.length <= 3 * 104 -105 <= nums[i] <= 105
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解
动态规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 var maxSubArray = function (nums ) let dp = nums[0 ]; let max = dp; for (let i = 1 ; i < nums.length; i++) { if (dp > 0 ) { dp += nums[i]; } else { dp = nums[i]; } max = Math .max(dp, max); } return max; };
改为分治法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 function Status (l, r, m, i ) this .lSum = l; this .rSum = r; this .mSum = m; this .iSum = i; } const pushUp = (l, r ) => { const iSum = l.iSum + r.iSum; const lSum = Math .max(l.lSum, l.iSum + r.lSum); const rSum = Math .max(r.rSum, r.iSum + l.rSum); const mSum = Math .max(Math .max(l.mSum, r.mSum), l.rSum + r.lSum); return new Status(lSum, rSum, mSum, iSum); } const getInfo = (a, l, r ) => { if (l === r) { return new Status(a[l], a[l], a[l], a[l]); } const m = (l + r) >> 1 ; const lSub = getInfo(a, l, m); const rSub = getInfo(a, m + 1 , r); return pushUp(lSub, rSub); } var maxSubArray = function (nums ) return getInfo(nums, 0 , nums.length - 1 ).mSum; };
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。
示例 1:
示例 2:
限制:
统计每一位的1的个数
1 2 3 4 5 6 7 8 9 10 11 12 var countDigitOne = function (n ) let counter = 0 ; for (let i = 1 ; i <= n; i *= 10 ){ let divider = 10 * i; counter += Math .floor(n / divider) * i + Math .min(Math .max(n % divider - i + 1 , 0 ), i); } return counter; };
数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中,第5位(从下标0开始计数)是5,第13位是1,第19位是4,等等。
请写一个函数,求任意第n位对应的数字。
示例 1:
示例 2:
限制:
模拟这个流程,先找到对应数的位数,再找到具体是哪个数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 var findNthDigit = function (n ) if (n == 0 ) return n; n--; let index = 1 ; let base = 9 ; while (n > index * base){ n -= index * base; index ++; base *= 10 ; } let num = Math .floor(n / index) + base / 9 ; let len = n % index; return num.toString()[len]; };
输入一个非负整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
示例 1:
示例 2:
1 2 输入: [3,30,34,5,9] 输出: "3033459"
提示:
说明:
输出结果可能非常大,所以你需要返回一个字符串而不是整数
拼接起来的数字可能会有前导 0,最后结果不需要去掉前导 0
构建一种新的排序方法进行数组排序,最后进行拼接
1 2 3 4 5 6 7 8 var minNumber = function (nums ) nums.sort((a, b ) => parseInt (a + '' + b) - parseInt (b + '' + a)); return nums.join("" ); };
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
示例 1:
1 2 3 输入: 12258 输出: 5 解释: 12258有5种不同的翻译,分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"
提示:
动态规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var translateNum = function (num ) num += "" ; if (num.length == 1 ) return 1 ; let dp1 = 1 , dp2 = 1 , dp3; for (let i = 1 ; i < num.length; i++){ if (parseInt ('' + num[i - 1 ] + num[i]) < 26 && num[i - 1 ] !== '0' ){ dp3 = dp1 + dp2; } else { dp3 = dp2; } dp1 = dp2; dp2 = dp3; } return dp3; };
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
1 2 3 4 5 6 7 8 输入: [ [1,3,1], [1,5,1], [4,2,1] ] 输出: 12 解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
0 < grid.length <= 2000 < grid[0].length <= 200
动态规划
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 var maxValue = function (grid ) if (grid == null ) return null ; let lenX = grid.length; let lenY = grid[0 ].length; let dp = []; for (let i = 0 ; i < lenX; i++){ dp[i] = []; for (let j = 0 ; j < lenY; j++){ if (i != 0 && j != 0 ) { dp[i][j] = Math .max(dp[i - 1 ][j], dp[i][j - 1 ]) + grid[i][j]; } else if (i == 0 && j == 0 ) { dp[i][j] = grid[i][j]; } else if (i == 0 ) { dp[i][j] = dp[i][j - 1 ] + grid[i][j]; } else { dp[i][j] = dp[i - 1 ][j] + grid[i][j]; } } } return dp[lenX - 1 ][lenY - 1 ]; };
路径压缩
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 var maxValue = function (grid ) let result = [], m = grid.length, n = grid[0 ].length; for (let i = 0 ; i < m; i++) { for (let j = 0 ; j < n; j++) { if (i == 0 && j === 0 ) { result[j] = grid[i][j]; continue ; } if (i === 0 ) { result[j] = result[j - 1 ] + grid[i][j]; continue ; } if (j === 0 ) { result[j] = result[j] + grid[i][j]; continue ; } result[j] = Math .max(result[j - 1 ], result[j]) + grid[i][j]; } } return result[n - 1 ]; };
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 1:
1 2 3 输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
1 2 3 输入: "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
1 2 3 4 输入: "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示:
使用滑动窗口
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 var lengthOfLongestSubstring = function (s ) let window = {}; let left = 0 , right = 0 ; let res = 0 ; while (right < s.length) { let c = s[right]; right++; if (window [c]) { window [c]++; } else { window [c] = 1 ; } while (window [c] > 1 ) { let d = s[left]; left++; window [d]--; } res = Math .max(res, right - left); } return res; };
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是只包含质因数 2、3 和/或 5 的正整数。
示例 1:
输入:n = 10
示例 2:
输入:n = 1
提示:
1 <= n <= 1690
3个指针分别指向当前2、3、5对应的数,找到最小值,进行指针移动,注意,指针可能同时拥有3个最小值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 var nthUglyNumber = function (n ) if (n == 0 ) return 0 ; let index2 = 0 , index3 = 0 , index5 = 0 ; var s = [1 ]; while (s.length < n){ let ugly = Math .min(2 * s[index2], 3 * s[index3], 5 * s[index5]); s.push(ugly); if (ugly == 2 * s[index2]) index2++; if (ugly == 3 * s[index3]) index3++; if (ugly == 5 * s[index5]) index5++; } return s[n - 1 ]; };
在字符串 s 中找出第一个只出现一次的字符。如果没有,返回一个单空格。 s 只包含小写字母。
示例:
1 2 3 4 5 s = "abaccdeff" 返回 "b" s = "" 返回 " "
限制:
使用哈希表或数组存储数量
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var firstUniqChar = function (s ) let count = {}; for (let i = 0 ; i < s.length; i++) { let char = s[i]; if (count[char] !== undefined ) { count[char]++; } else { count[char] = 1 ; } } for (let i = 0 ; i < s.length; i++) { let char = s[i]; if (count[char] === 1 ) { return char; } } return ' ' ; }
改成数组形式
1 2 3 4 5 6 7 8 9 10 11 12 13 var firstUniqChar = function (s ) let arr = new Array (26 ).fill(0 ); let charCodeAtA = 'a' .charCodeAt(); for (let c of s) { arr[c.charCodeAt() - charCodeAtA]++; } for (let c of s) { if (arr[c.charCodeAt() - charCodeAtA] === 1 ) { return c; } } return " " ; };
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
示例 1:
限制:
使用类似归并排序的方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 var reversePairs = function (nums ) let n = nums.length; let tmp = new Array (n); return mergeSort(nums, tmp, 0 ,n - 1 ); }; function mergeSort (nums, tmp, l, r ) if (l >= r) return 0 ; let mid = l + ((r - l) >> 1 ); let inv_count = mergeSort(nums, tmp, l, mid) + mergeSort(nums, tmp, mid + 1 , r); let i = l, j = mid + 1 , pos = l; while (i <= mid && j <= r) { if (nums[i] <= nums[j]) { tmp[pos] = nums[i]; i++; inv_count += (j - (mid + 1 )); } else { tmp[pos] = nums[j]; j++; } pos++; } for (let k = i; k <= mid; k++) { tmp[pos++] = nums[k]; inv_count += (j - (mid + 1 )); } for (let k = j; k <= r; k++) { tmp[pos++] = nums[k]; } for (let k = l; k <= r; k++) { nums[k] = tmp[k]; } return inv_count; }
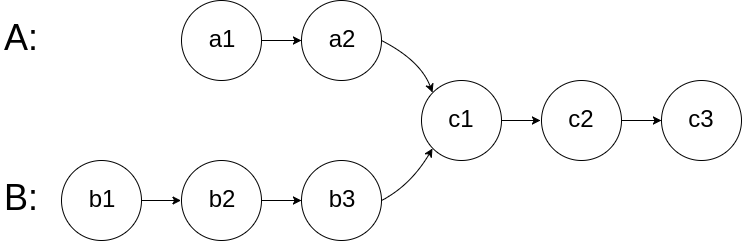
输入两个链表,找出它们的第一个公共节点。
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
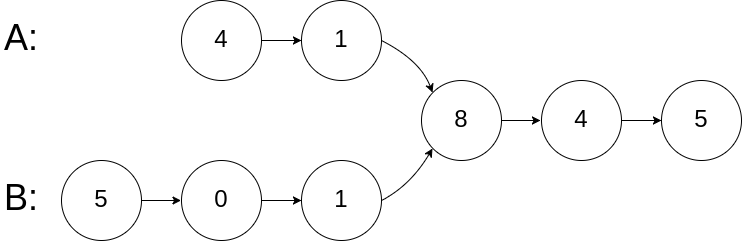
1 2 3 输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3 输出:Reference of the node with value = 8 输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
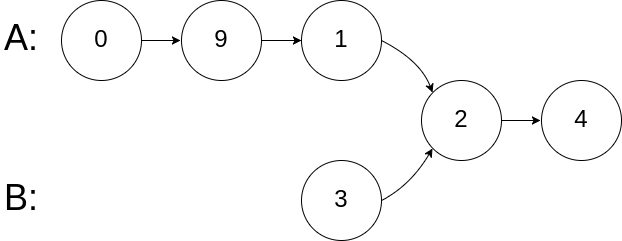
1 2 3 输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Reference of the node with value = 2 输入解释:相交节点的值为 2 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
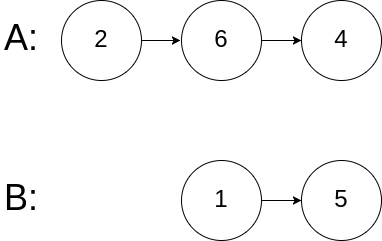
1 2 3 4 输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:null 输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 解释:这两个链表不相交,因此返回 null。
注意:
如果两个链表没有交点,返回 null.
在返回结果后,两个链表仍须保持原有的结构。
可假定整个链表结构中没有循环。
程序尽量满足 O(n ) 时间复杂度,且仅用 O(1 ) 内存。
双指针,走到头换一条链表继续
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 var getIntersectionNode = function (headA, headB ) let pointA = headA, pointB = headB; while (pointA !== pointB) { pointA = pointA ? pointA.next: headB; pointB = pointB ? pointB.next: headA; } return pointA; };
哈希表记录每个点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 var getIntersectionNode = function (headA, headB ) const map = new Map (); let node = headA; while (node) { map.set(node, true ); node = node.next; } node = headB; while (node) { if (map.has(node)) { return node; } node = node.next; } return null ; };
统计一个数字在排序数组中出现的次数。
示例 1:
1 2 输入: nums = [5,7,7,8,8,10], target = 8 输出: 2
示例 2:
1 2 输入: nums = [5,7,7,8,8,10], target = 6 输出: 0
限制:
使用二分查找分别找到上边界和下边界
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 var search = function (nums, target ) let left1 = 0 , right1 = nums.length - 1 ; while (left1 <= right1) { let mid = left1 + ((right1 - left1) >> 1 ); if (nums[mid] === target) { right1 = mid - 1 ; } else if (nums[mid] > target) { right1 = mid - 1 ; } else if (nums[mid] < target) { left1 = mid + 1 ; } } if (left1 >= nums.length || nums[left1] !== target) { return 0 ; } let left2 = 0 , right2 = nums.length - 1 ; while (left2 <= right2) { let mid = left2 + ((right2 - left2) >> 1 ); if (nums[mid] === target) { left2 = mid + 1 ; } else if (nums[mid] > target) { right2 = mid - 1 ; } else if (nums[mid] < target) { left2 = mid + 1 ; } } return right2 - left1 + 1 ; };
找到一个直接遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 var search = function (nums, target ) let temp = -1 ; for (let l = 0 , r = nums.length - 1 ; l <= r;) { let mid = (l + r) >>> 1 ; if (nums[mid] < target) { l = mid + 1 ; } else if (nums[mid] > target) { r = mid - 1 ; } else { temp = mid; break ; } } if (temp === -1 ) { return 0 ; } let count = 0 ; for (let i = temp; nums[i] === target; i--) { count++; } for (let i = temp + 1 ; nums[i] === target; i++) { count++; } return count; };
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
示例 1:
示例 2:
1 2 输入: [0,1,2,3,4,5,6,7,9] 输出: 8
限制:
二分查找,找到第一个nums[index] !== index的结果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 var missingNumber = function (nums ) let left = 0 , right = nums.length - 1 ; while (left <= right){ let mid = (left + right) >> 1 ; if (nums[mid] === mid) { left = mid + 1 ; } else { right = mid - 1 ; } } return left; };
位运算
1 2 3 4 5 6 7 8 9 10 11 12 var missingNumber = function (nums ) let res = nums.length; nums.forEach(function (item, index ) res ^= item; res ^= index; }); return res; };
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
1 2 3 4 5 6 7 输入: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 输出: 4
示例 2:
1 2 3 4 5 6 7 8 9 输入: root = [5,3,6,2,4,null,null,1], k = 3 5 / \ 3 6 / \ 2 4 / 1 输出: 4
限制:
1 ≤ k ≤ 二叉搜索树元素个数
对于二叉搜索树来说,就是反向中序遍历找第k个数,可以使用递归法和迭代法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 var kthLargest = function (root, k ) if (!root) return null ; let cur = root; let count = 0 , stack = []; while (cur || stack.length) { while (cur) { stack.push(cur); cur = cur.right; } cur = stack.pop(); count++; if (count === k) { return cur.val; } cur = cur.left; } return null ; };
递归法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 var kthLargest = function (root, k ) let stack = []; var lastOrder = function (root ) if (root === null ) return ; lastOrder(root.right); stack.push(root.val); lastOrder(root.left); } lastOrder(root); return stack[k - 1 ]; };
输入一棵二叉树的根节点,求该树的深度。从根节点到叶节点依次经过的节点(含根、叶节点)形成树的一条路径,最长路径的长度为树的深度。
例如:
给定二叉树 [3,9,20,null,null,15,7],
返回它的最大深度 3 。
提示:
节点总数 <= 10000
采用递归法
1 2 3 4 var maxDepth = function (root ) if (root === null ) return 0 ; return Math .max(maxDepth(root.left), maxDepth(root.right)) + 1 ; };
递归剪枝
1 2 3 4 5 6 7 8 9 10 11 12 13 var maxDepth = function (root ) if (!root) return 0 ; let max = 0 ; function deepFun (node, d ) if (!node.left && !node.right){ if (max < d + 1 ) max = d + 1 ; } if (node.left) deepFun(node.left, d + 1 ); if (node.right) deepFun(node.right, d + 1 ); } deepFun(root, 0 ); return max; }
输入一棵二叉树的根节点,判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:
1 2 输入:root = [3,9,20,null,null,15,7] 输出:true
示例 2:
1 2 输入:root = [1,2,2,3,3,null,null,4,4] 输出:false
示例 3:
提示:
树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104
递归计算某节点深度及遍历深度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 var isBalanced = function (root ) function recur (root ) if (!root) return 0 ; let left = recur(root.left); if (left === -1 ) return -1 ; let right = recur(root.right); if (right === -1 ) return -1 ; if (Math .abs(left - right) <= 1 ) { return Math .max(left, right) + 1 ; } else { return -1 ; } } return recur(root) !== -1 ; };
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
示例 1:
1 2 输入:nums = [4,1,4,6] 输出:[1,6] 或 [6,1]
示例 2:
1 2 输入:nums = [1,2,10,4,1,4,3,3] 输出:[2,10] 或 [10,2]
限制:
2 <= nums.length <= 10000
使用位运算异或得到两个数异或的结果,然后将该结果最后一位相与结果不为0或者结果为0的进行异或
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 var singleNumbers = function (nums ) let res = nums.reduce((a, b ) => a ^ b); let num = res & -res; let a = 0 ; let b = 0 ; nums.forEach(value => if (value & num) { a ^= value; } else { b ^= value; } }) return [a, b]; };
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
示例 1:
1 2 输入:nums = [3,4,3,3] 输出:4
示例 2:
1 2 输入:nums = [9,1,7,9,7,9,7] 输出:1
限制:
1 <= nums.length <= 100001 <= nums[i] < 2^31
如下图所示,考虑数字的二进制形式,对于出现三次的数字,各 二进制位 出现的次数都是 3 的倍数。
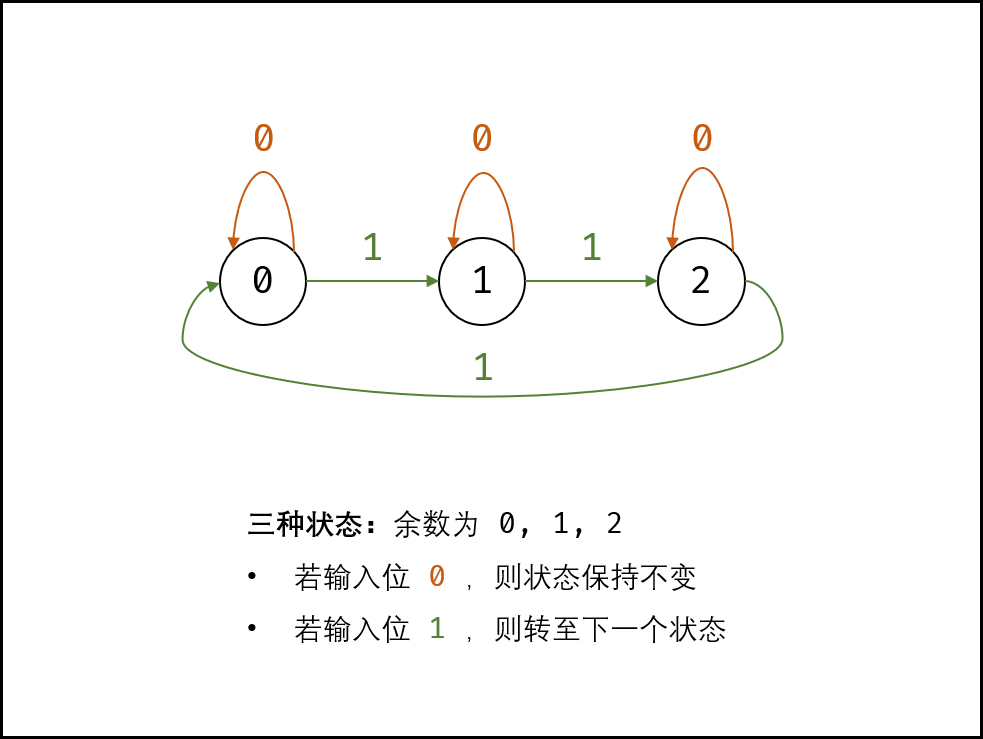
各二进制位的 位运算规则相同 ,因此只需考虑一位即可。如下图所示,对于所有数字中的某二进制位 11 的个数,存在 3 种状态,即对 3 余数为 0, 1, 2 。
若输入二进制位 1 ,则状态按照以下顺序转换;
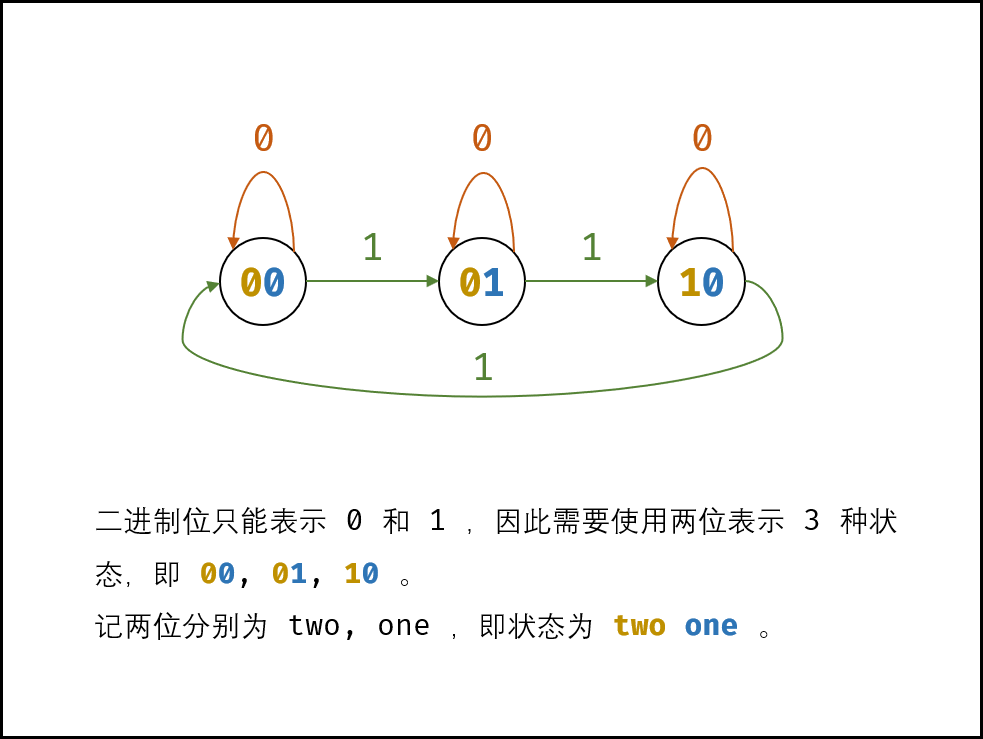
如下图所示,由于二进制只能表示 0, 1,因此需要使用两个二进制位来表示 3 个状态。设此两位分别为 two , one ,则状态转换变为:
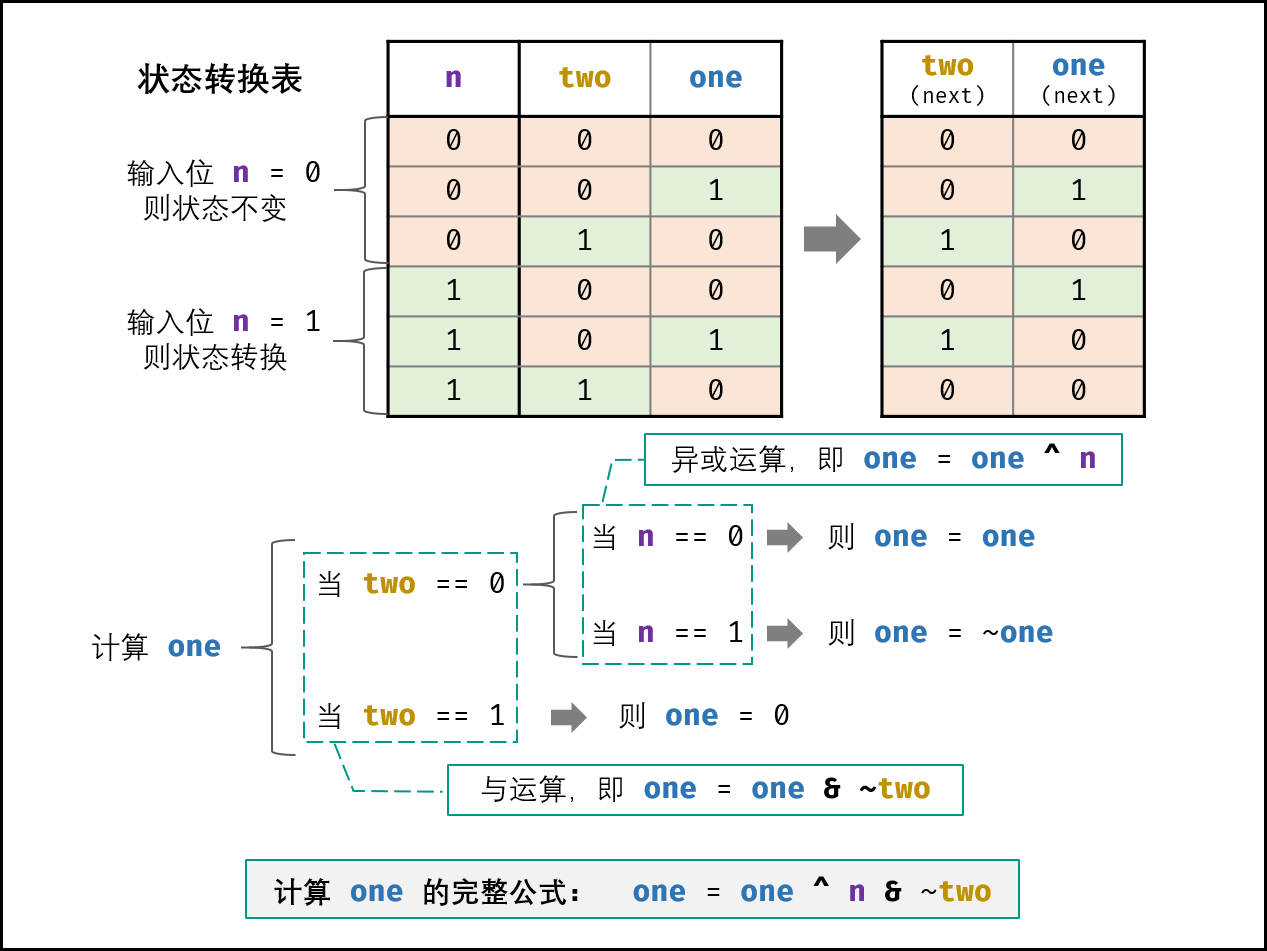
接下来,需要通过 状态转换表 导出 状态转换的计算公式 。首先回忆一下位运算特点,对于任意二进制位 x ,有:
异或运算:x ^ 0 = x , x ^ 1 = ~x
设当前状态为 two one ,此时输入二进制位 n 。如下图所示,通过对状态表的情况拆分,可推出 one 的计算方法为:
if two == 0:
if two == 0:
one = one ^ n & ~two
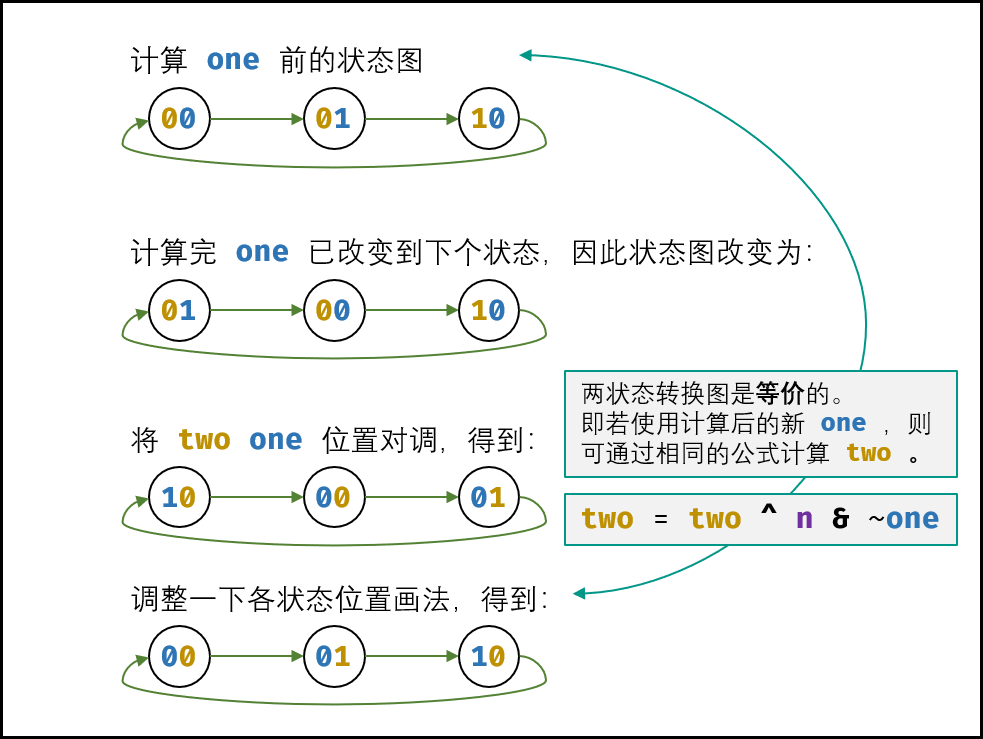
计算 two 方法:
由于是先计算 one ,因此应在新 one 的基础上计算 two 。
two = two ^ n & ~one
返回值:
以上是对数字的二进制中 “一位” 的分析,而 int 类型的其他 31 位具有相同的运算规则,因此可将以上公式直接套用在 32 位数上。
遍历完所有数字后,各二进制位都处于状态 00 和状态 010 (取决于 “只出现一次的数字” 的各二进制位是 11 还是 00 ),而此两状态是由 one 来记录的(此两状态下 twos 恒为 00 ),因此返回 ones 即可。
复杂度分析:
1 2 3 4 5 6 7 8 9 10 11 12 var singleNumber = function (nums ) let ones = 0 , twos = 0 ; for (let i = 0 ; i < nums.length; i++){ ones = ones ^ nums[i] & ~twos; twos = twos ^ nums[i] & ~ones; } return ones; };
输入一个递增排序的数组和一个数字s,在数组中查找两个数,使得它们的和正好是s。如果有多对数字的和等于s,则输出任意一对即可。
示例 1:
1 2 输入:nums = [2,7,11,15], target = 9 输出:[2,7] 或者 [7,2]
示例 2:
1 2 输入:nums = [10,26,30,31,47,60], target = 40 输出:[10,30] 或者 [30,10]
限制:
1 <= nums.length <= 10^51 <= nums[i] <= 10^6
双指针
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 var twoSum = function (nums, target ) let l = 0 ; let r = nums.length - 1 ; while (l < r) { if (nums[l] + nums[r] > target) { r--; } else if (nums[l] + nums[r] === target){ return [nums[l], nums[r]]; } else if (nums[l] + nums[r] < target){ l++; } } };
输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。
序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
示例 1:
1 2 输入:target = 9 输出:[[2,3,4],[4,5]]
示例 2:
1 2 输入:target = 15 输出:[[1,2,3,4,5],[4,5,6],[7,8]]
限制:
数学方法,找到最小的数和中间数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 var findContinuousSequence = function (target ) let number = []; let i = 2 * Math .floor(Math .sqrt(target)) - 1 ; for (; i > 1 ; i--){ let inc = i * (i - 1 ) / 2 ; if ((target - inc) % i === 0 && (target - inc) / i > 0 ) number.push(new Array (i).fill("" ).map((item, index ) => index + (target - inc) / i)); } return number; }
输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。为简单起见,标点符号和普通字母一样处理。例如输入字符串”I am a student. “,则输出”student. a am I”。
示例 1:
1 2 输入: "the sky is blue" 输出: "blue is sky the"
示例 2:
1 2 3 输入: " hello world! " 输出: "world! hello" 解释: 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
示例 3:
1 2 3 输入: "a good example" 输出: "example good a" 解释: 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
说明:
无空格字符构成一个单词。
输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
这种题JS真心方便
1 2 3 4 5 6 7 var reverseWords = function (s ) return s.trim().split(/\s+/ ).reverse().join(" " ); };
优化一下效率
1 2 3 4 5 6 7 var reverseWords = function (s ) return s.trim().split(/\s\s*/ ).reverse().join(" " ); };
字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如,输入字符串”abcdefg”和数字2,该函数将返回左旋转两位得到的结果”cdefgab”。
示例 1:
1 2 输入: s = "abcdefg", k = 2 输出: "cdefgab"
示例 2:
1 2 输入: s = "lrloseumgh", k = 6 输出: "umghlrlose"
限制:
1 <= k < s.length <= 10000
第n个字符后的拼接n个字符之前的
1 2 3 4 5 6 7 8 var reverseLeftWords = function (s, n ) return s.slice(n).concat(s.slice(0 , n)); };
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。
示例:
1 2 3 4 5 6 7 8 9 10 11 12 输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3 输出: [3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 ------------------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7
提示:
你可以假设 k 总是有效的,在输入数组不为空的情况下,1 ≤ k ≤ 输入数组的大小。
使用单调队列记录k个数中的最大值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 var maxSlidingWindow = function (nums, k ) let deque = [], ans = []; for (let i = 0 ; i < nums.length; i++) { if (i >= k && deque[0 ] <= i - k) deque.shift(); while (deque.length && nums[i] >= nums[deque[deque.length - 1 ]]) deque.pop(); deque.push(i); if (i >= k - 1 ) ans.push(nums[deque[0 ]]); } return ans; };
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊 时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
示例 1:
1 2 3 4 输入: ["MaxQueue","push_back","push_back","max_value","pop_front","max_value"] [[],[1],[2],[],[],[]] 输出: [null,null,null,2,1,2]
示例 2:
1 2 3 4 输入: ["MaxQueue","pop_front","max_value"] [[],[],[]] 输出: [null,-1,-1]
限制:
1 <= push_back,pop_front,max_value的总操作数 <= 100001 <= value <= 10^5
按照定义,进行队列操作
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 var MaxQueue = function ( this .data = []; this .maxQueue = []; }; MaxQueue.prototype.max_value = function ( if (this .data.length === 0 ) { return -1 ; } else { return this .maxQueue[0 ]; } }; MaxQueue.prototype.push_back = function (value ) this .data.push(value); while (this .maxQueue.length !== 0 && this .maxQueue[this .maxQueue.length - 1 ] < value) { this .maxQueue.pop(); } this .maxQueue.push(value); }; MaxQueue.prototype.pop_front = function ( if (this .data.length === 0 ) return -1 ; let data_temp = this .data.shift(); if (data_temp === this .maxQueue[0 ]) this .maxQueue.shift(); return data_temp; };
把n个骰子扔在地上,所有骰子朝上一面的点数之和为s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
1 2 输入: 1 输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
1 2 输入: 2 输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
限制:
采用动态规划,dp[i]是和为i的个数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 var twoSum = function (n ) const dp = new Array (70 ).fill(0 ); const res = []; for (let i = 1 ; i <= 6 ; i++) { dp[i] = 1 ; } for (let round = 2 ; round <= n; round++) { for (let count = 6 * round; count >= round; count--) { dp[count] = 0 ; for (let j = 1 ; j <= 6 ; j++) { if (count - j < round - 1 ) { break ; } dp[count] += dp[count - j]; } } } const all = Math .pow(6 , n); for (let total = n; total <= 6 * n; total++) { res.push(dp[total] * 1.0 / all); } return res; };
0,1,···,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字(删除后从下一个数字开始计数)。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
示例 1:
示例 2:
1 2 输入: n = 10, m = 17 输出: 2
限制:
1 <= n <= 10^51 <= m <= 10^6
数学解法
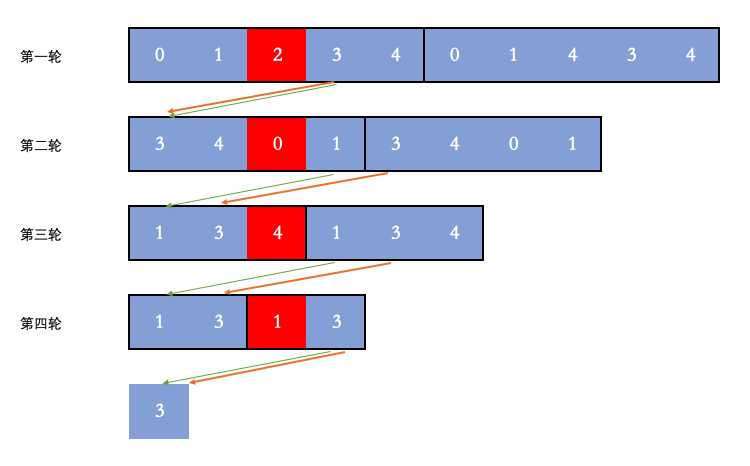
因为数据是放在数组里,所以我在数组后面加上了数组的复制,以体现是环状的。我们先忽略图片里的箭头:
很明显我们每次删除的是第 m 个数字,我都标红了。
第一轮是 [0, 1, 2, 3, 4] ,所以是 [0, 1, 2, 3, 4] 这个数组的多个复制。这一轮 2 删除了。
第二轮开始时,从 3 开始,所以是 [3, 4, 0, 1] 这个数组的多个复制。这一轮 0 删除了。
第三轮开始时,从 1 开始,所以是 [1, 3, 4] 这个数组的多个复制。这一轮 4 删除了。
第四轮开始时,还是从 1 开始,所以是 [1, 3] 这个数组的多个复制。这一轮 1 删除了。
最后剩下的数字是 3。
图中的绿色的线指的是新的一轮的开头是怎么指定的,每次都是固定地向前移位 m 个位置。
然后我们从最后剩下的 3 倒着看,我们可以反向推出这个数字在之前每个轮次的位置。
最后剩下的 3 的下标是 0。
第四轮反推,补上 m 个位置,然后模上当时的数组大小 2,位置是(0 + 3) % 2 = 1。
第三轮反推,补上 m 个位置,然后模上当时的数组大小 3,位置是(1 + 3) % 3 = 1。
第二轮反推,补上 m 个位置,然后模上当时的数组大小 4,位置是(1 + 3) % 4 = 0。
第一轮反推,补上 m 个位置,然后模上当时的数组大小 5,位置是(0 + 3) % 5 = 3。
所以最终剩下的数字的下标就是3。因为数组是从0开始的,所以最终的答案就是3。
总结一下反推的过程,就是 (当前index + m) % 上一轮剩余数字的个数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 var lastRemaining = function (n, m ) let f = 0 ; for (let i = 2 ; i <= n; i++) { f = (f + m) % i; } return f; };
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
1 2 3 4 输入: [7,1,5,3,6,4] 输出: 5 解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
1 2 3 输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
限制:
动态规划,分别记录当前买入股票和卖出股票的最多钱
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 var maxProfit = function (prices ) let n = prices.length; let dp_i_0 = 0 , dp_i_1 = Number .MIN_SAFE_INTEGER; for (let i = 0 ; i < n; i++) { dp_i_0 = Math .max(dp_i_0, dp_i_1 + prices[i]); dp_i_1 = Math .max(dp_i_1, -prices[i]); } return dp_i_0; };
求 1+2+...+n ,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
示例 1:
示例 2:
限制:
利用&&的短路效应进行计算
1 2 3 4 5 6 7 var sumNums = function (n ) return n > 0 && (n + sumNums(n - 1 )); };
写一个函数,求两个整数之和,要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
示例:
提示:
a, b 均可能是负数或 0结果不会溢出 32 位整数
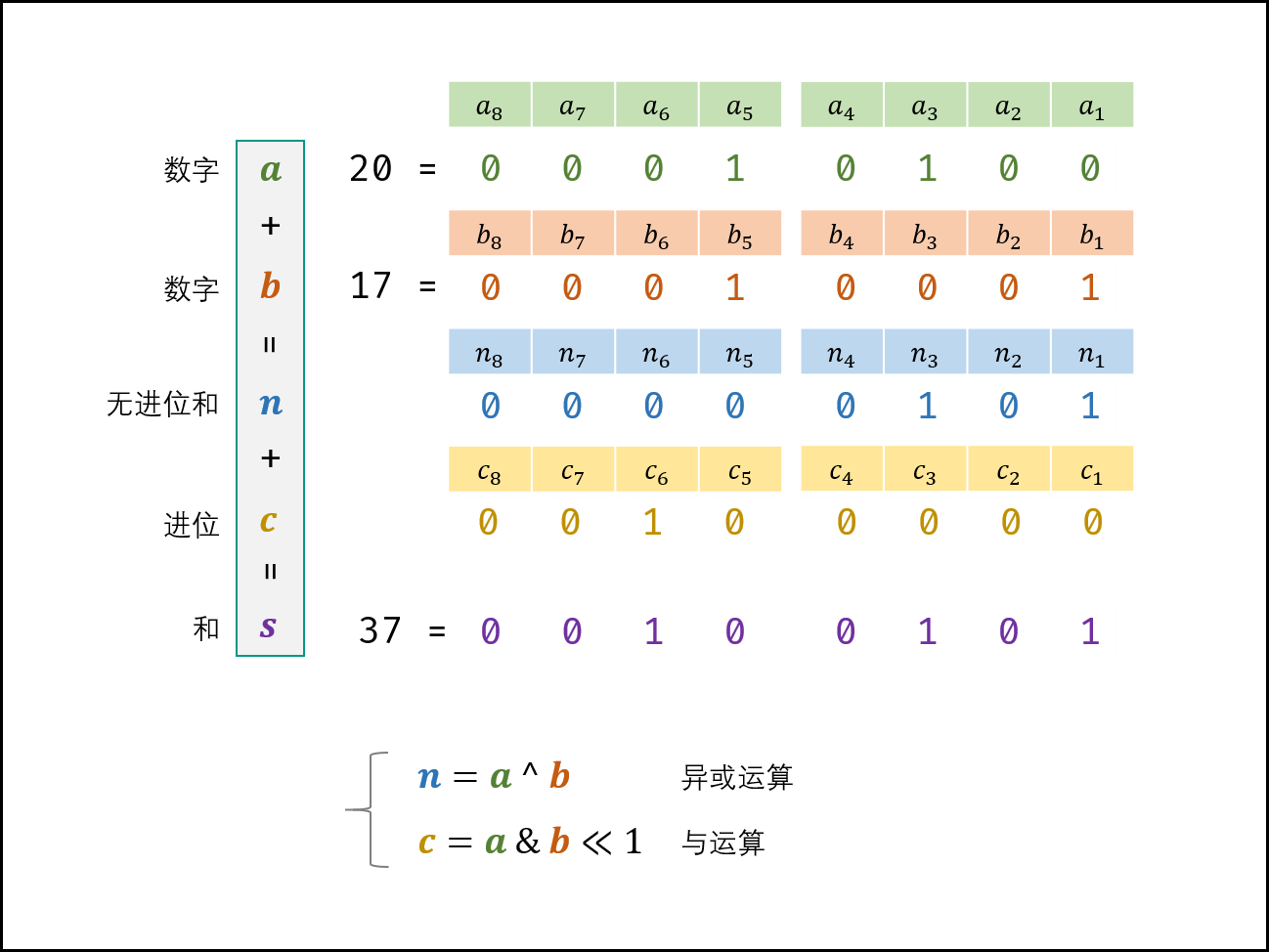
本题考察对位运算的灵活使用,即使用位运算实现加法。
a(i)
b(i)
无进位和 n(i)
进位 c(i+1)
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
观察发现,无进位和 与 异或运算 规律相同,进位 和 与运算 规律相同(并需左移一位)。因此,无进位和 n 与进位 c 的计算公式如下;
$$
1 2 3 4 5 6 7 8 9 10 11 12 13 var add = function (a, b ) while (b !== 0 ){ let c = (a & b) << 1 ; a ^= b; b = c; } return a; };
给定一个数组 A[0,1,…,n-1],请构建一个数组 B[0,1,…,n-1],其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。
示例:
1 2 输入: [1,2,3,4,5] 输出: [120,60,40,30,24]
提示:
所有元素乘积之和不会溢出 32 位整数
a.length <= 100000
不能用除法,先记录前面的数的乘积,再与后面的积相乘
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 var constructArr = function (a ) const len = a.length; if (len === 0 ) return []; let b = new Array (len).fill(1 ); for (let i = 1 ; i < len; i++){ b[i] = b[i - 1 ] * a[i - 1 ]; } let temp = 1 ; for (let j = len - 2 ; j >= 0 ; j--){ temp *= a[j + 1 ]; b[j] *= temp; } return b; };
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
读入字符串并丢弃无用的前导空格
检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。
如果整数数超过 32 位有符号整数范围 [$-2^{31}$,$2^{31}-1$],需要截断这个整数,使其保持在这个范围内。具体来说,小于 $-2^{31}$的整数应该被固定为 $-2^{31}$ ,大于$2^{31}-1$ 的整数应该被固定为$2^{31}-1$ 。
注意:
本题中的空白字符只包括空格字符 ‘ ‘ 。
除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 输入:s = "42" 输出:42 解释:加粗的字符串为已经读入的字符,插入符号是当前读取的字符。 第 1 步:"42"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"42"(读入 "42") ^ 解析得到整数 42 。 由于 "42" 在范围 [-231, 231 - 1] 内,最终结果为 42 。
示例 2:
1 2 3 4 5 6 7 8 9 10 11 输入:s = " -42" 输出:-42 解释: 第 1 步:" -42"(读入前导空格,但忽视掉) ^ 第 2 步:" -42"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:" -42"(读入 "42") ^ 解析得到整数 -42 。 由于 "-42" 在范围 [-231, 231 - 1] 内,最终结果为 -42 。
示例 3:
1 2 3 4 5 6 7 8 9 10 11 输入:s = "4193 with words" 输出:4193 解释: 第 1 步:"4193 with words"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"4193 with words"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"4193 with words"(读入 "4193";由于下一个字符不是一个数字,所以读入停止) ^ 解析得到整数 4193 。 由于 "4193" 在范围 [-231, 231 - 1] 内,最终结果为 4193 。
示例 4:
1 2 3 4 5 6 7 8 9 10 11 输入:s = "words and 987" 输出:0 解释: 第 1 步:"words and 987"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"words and 987"(当前没有读入字符,因为这里不存在 '-' 或者 '+') ^ 第 3 步:"words and 987"(由于当前字符 'w' 不是一个数字,所以读入停止) ^ 解析得到整数 0 ,因为没有读入任何数字。 由于 0 在范围 [-231, 231 - 1] 内,最终结果为 0 。
示例 5:
1 2 3 4 5 6 7 8 9 10 11 输入:s = "-91283472332" 输出:-2147483648 解释: 第 1 步:"-91283472332"(当前没有读入字符,因为没有前导空格) ^ 第 2 步:"-91283472332"(读入 '-' 字符,所以结果应该是负数) ^ 第 3 步:"-91283472332"(读入 "91283472332") ^ 解析得到整数 -91283472332 。 由于 -91283472332 小于范围 [-231, 231 - 1] 的下界,最终结果被截断为 -231 = -2147483648 。
提示:
0 <= s.length <= 200
利用parseInt实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 var myAtoi = function (str ) const number = parseInt (str, 10 ); if (number > Math .pow(2 , 31 ) - 1 ) { return Math .pow(2 , 31 ) - 1 ; } else if (number < Math .pow(-2 , 31 )) { return Math .pow(-2 , 31 ); } else if (isNaN (number)) { return 0 ; } else { return number; } };
利用封装状态机实现,实在是太复杂了,我当时详细写了一般注释
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 var strToInt = function (str ) class Automation constructor ( this .state = 'start' ; this .sign = 1 ; this .answer = 0 ; this .map = new Map ([ ['start' , ['start' , 'signed' , 'in_number' , 'end' ]], ['signed' , ['end' , 'end' , 'in_number' , 'end' ]], ['in_number' , ['end' , 'end' , 'in_number' , 'end' ]], ['end' , ['end' , 'end' , 'end' , 'end' ]] ]); } getIndex (char ) if (char === ' ' ) { return 0 ; } else if (char === '-' || char === '+' ) { return 1 ; } else if (typeof Number (char) === 'number' && !isNaN (char)) { return 2 ; } else { return 3 ; } } get (char ) this .state = this .map.get(this .state)[this .getIndex(char)]; if (this .state === 'in_number' ) { this .answer = this .answer * 10 + (char - 0 ); this .answer = this .sign === 1 ? Math .min(this .answer, Math .pow(2 , 31 ) - 1 ) : Math .min(this .answer, -Math .pow(-2 , 31 )); } else if (this .state === 'signed' ) { this .sign = char === '+' ? 1 : -1 ; } } } let automation = new Automation(); for (let char of str) { automation.get(char); } return automation.sign * automation.answer; };
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科 中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先 )。”
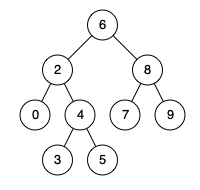
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
1 2 3 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
1 2 3 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
递归查询
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 var lowestCommonAncestor = function (root, p, q ) if (!root) return null ; if (root.val >= Math .min(p.val, q.val) && root.val <= Math .max(p.val, q.val)) return root; return lowestCommonAncestor(root.left, p, q) || lowestCommonAncestor(root.right, p, q); };
将递归转为迭代
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var lowestCommonAncestor = function (root, p, q ) let ancestor = root; while (true ) { if (p.val < ancestor.val && q.val < ancestor.val) { ancestor = ancestor.left; } else if (p.val > ancestor.val && q.val > ancestor.val) { ancestor = ancestor.right; } else { break ; } } return ancestor; };
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
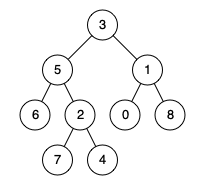
1 2 3 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
1 2 3 输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
1 2 输入:root = [1,2], p = 1, q = 2 输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
递归查询公共父节点,要么p 和 q 两者之一是另一个父节点,要么保证p 和 q 在当前节点两个子节点之中
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var lowestCommonAncestor = function (root, p, q ) if (root == null || root == p || root == q) return root; let left = lowestCommonAncestor(root.left, p, q); let right = lowestCommonAncestor(root.right, p, q); if (left && right) return root; return left || right; };


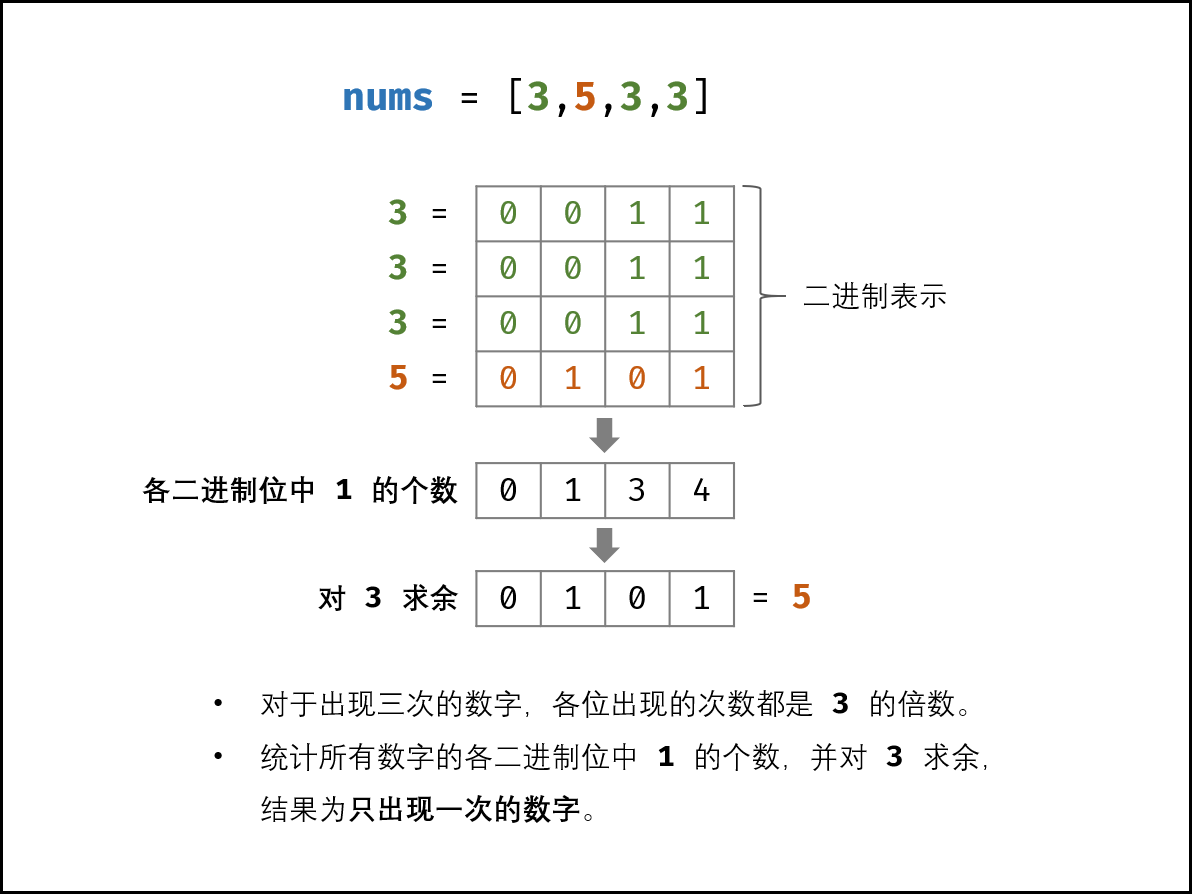 因此,统计所有数字的各二进制位中 1 的出现次数,并对 3 求余,结果则为只出现一次的数字。
因此,统计所有数字的各二进制位中 1 的出现次数,并对 3 求余,结果则为只出现一次的数字。