hxy的博客

Mia san Mia!

0%

其他刷题

发表于 更新于 分类于 Valine：

按照算法和数据结构进行分类，一起来刷题，用于自己在面试前查漏补缺。我的意向岗位是前端，选择用javascript来刷题，优点是动态语言，语法简单，缺点是遇见复杂数据结构会出现较难的写法，如堆、并查集，每题对应leetcode的题号。本篇是其他

专题部分

不知道怎么分类的

48. 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

img

1
2
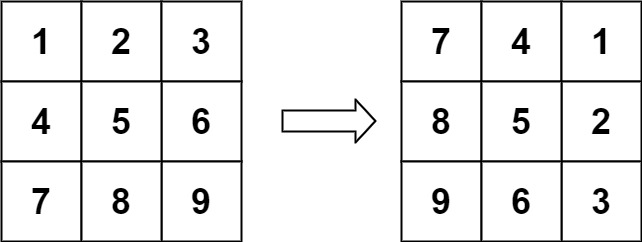
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

img

1
2
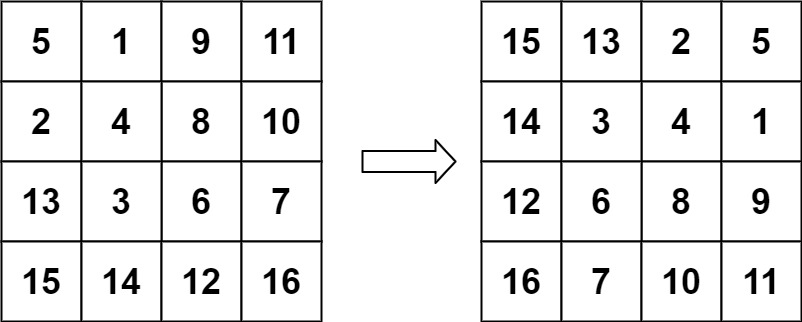
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

示例 3：

1
2
输入：matrix = [[1]]
输出：[[1]]

示例 4：

1
2
输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]

提示：

  • matrix.length == n
  • matrix[i].length == n
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

可以四个对应的点一起旋转，不过写起来费脑子，我是喜欢上下翻折加对角线翻折

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var rotate = function(arr) {
    let vecor = arr.length;
    // 垂直翻转
    for (let i = 0, len = vecor / 2; i < len; i++) {
        for (let j = 0, tmp; j < vecor; j++) {
            tmp = arr[i][j];
            arr[i][j] = arr[vecor - i - 1][j];
            arr[vecor - i - 1][j] = tmp;
        }
    }
    // 对角线翻转
    for (let i = 0; i < vecor; i++) {
        for (let j = 0, tmp; j < i; j++) {
            tmp = arr[i][j];
            arr[i][j] = arr[j][i];
            arr[j][i] = tmp;
        }
    }
    return arr;
};

四个点一组旋转的代码我是抄，用两个双指针确实比较好想一些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var rotate = function(matrix) {
    let l = matrix.length;
    for (let start = 0, end = l - 1; start < end; start++, end--) {
        for (let s = start, e = end; s < end; s++, e--) {
            let temp = matrix[start][s];
            matrix[start][s] = matrix[e][start];
            matrix[e][start] = matrix[end][e];
            matrix[end][e] = matrix[s][end];
            matrix[s][end] = temp;
        }
    }
};

208. 实现 Trie (前缀树)

Trie**（发音类似 “try”）或者说 **前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

  • Trie() 初始化前缀树对象。
  • void insert(String word) 向前缀树中插入字符串 word 。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

提示：

  • 1 <= word.length, prefix.length <= 2000
  • word 和 prefix 仅由小写英文字母组成
  • insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次

ES6语法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Trie {
    constructor() {
        this.root = Object.create(null);
    }
    insert(word) {
        let node = this.root;
        for (const c of word) {
            if (!node[c]) node[c] = Object.create(null);
            node = node[c];
        }
        node.isWord = true;
    }
    traverse(word) {
        let node = this.root;
        for (const c of word) {
            node = node[c];
            if (!node) return null;
        }
        return node;
    }
    search(word) {
        const node = this.traverse(word);
        return !!node && !!node.isWord;
    }
    startsWith(prefix) {
        return !!this.traverse(prefix);
    }
};

ES5语法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
var TrieNode = function() {
    this.next = {};
    this.isEnd = false;
};

/**
 * Initialize your data structure here.
 */
var Trie = function() {
    this.root = new TrieNode();
};

/**
 * Inserts a word into the trie. 
 * @param {string} word
 * @return {void}
 */
Trie.prototype.insert = function(word) {
    if (!word) return false;

    let node = this.root;
    for (let i = 0; i < word.length; i++) {
        if (!node.next[word[i]]) {
            node.next[word[i]] = new TrieNode();
        }
        node = node.next[word[i]];
    }
    node.isEnd = true;
    return true;
};

/**
 * Returns if the word is in the trie. 
 * @param {string} word
 * @return {boolean}
 */
Trie.prototype.search = function(word) {
    if (!word) return false;

    let node = this.root;
    for (let i = 0; i < word.length; i++) {
        if (node.next[word[i]]) {
            node = node.next[word[i]];
        } else {
            return false;
        }       
    }
    return node.isEnd;
};

/**
 * Returns if there is any word in the trie that starts with the given prefix. 
 * @param {string} prefix
 * @return {boolean}
 */
Trie.prototype.startsWith = function(prefix) {
    if (!prefix) return false;

    let node = this.root;
    for (let i = 0; i < prefix.length; i++) {
        if (node.next[prefix[i]]) {
            node = node.next[prefix[i]];
        } else {
            return false;
        }       
    }
    return true;
};

/**
 * Your Trie object will be instantiated and called as such:
 * var obj = new Trie()
 * obj.insert(word)
 * var param_2 = obj.search(word)
 * var param_3 = obj.startsWith(prefix)
 */

448. 找到所有数组中消失的数字

给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果。

示例 1：

1
2
输入：nums = [4,3,2,7,8,2,3,1]
输出：[5,6]

示例 2：

1
2
输入：nums = [1,1]
输出：[2]

提示：

  • n == nums.length
  • 1 <= n <= 105
  • 1 <= nums[i] <= n

进阶：你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。

标志位转为负数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number[]} nums
 * @return {number[]}
 */
var findDisappearedNumbers = function(nums) {
    let ans = [];
    for (let num of nums) {
        let pos = Math.abs(num) - 1;
        if (nums[pos] > 0) {
            nums[pos] = -nums[pos];
        }
    }
    for (let i = 0; i < nums.length; i++) {
        if (nums[i] > 0) {
            ans.push(i + 1);
        }
    }

    return ans;
};

621. 任务调度器

给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行，并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间，CPU 可以完成一个任务，或者处于待命状态。

然而，两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间，因此至少有连续 n 个单位时间内 CPU 在执行不同的任务，或者在待命状态。

你需要计算完成所有任务所需要的 最短时间 。

示例 1：

1
2
3
4
输入：tasks = ["A","A","A","B","B","B"], n = 2
输出：8
解释：A -> B -> (待命) -> A -> B -> (待命) -> A -> B
     在本示例中，两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间，而执行一个任务只需要一个单位时间，所以中间出现了（待命）状态。

示例 2：

1
2
3
4
5
6
7
8
输入：tasks = ["A","A","A","B","B","B"], n = 0
输出：6
解释：在这种情况下，任何大小为 6 的排列都可以满足要求，因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类

示例 3：

1
2
3
4
输入：tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出：16
解释：一种可能的解决方案是：
     A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A

提示：

  • 1 <= task.length <= 104
  • tasks[i] 是大写英文字母
  • n 的取值范围为 [0, 100]

模拟

一种容易想到的方法是，我们按照时间顺序，依次给每一个时间单位分配任务。

那么如果当前有多种任务不在冷却中，那么我们应该如何挑选执行的任务呢？直觉上，我们应当选择剩余执行次数最多的那个任务，将每种任务的剩余执行次数尽可能平均，使得 CPU 处于待命状态的时间尽可能少。当然这也是可以证明的，详细证明见下一个小标题。

因此我们可以用二元组 $$(\textit{nextValid}_i, \textit{rest}_i)$$ 表示第 $$i$$ 个任务，其中 $$\textit{nextValid}_i$$表示其因冷却限制，最早可以执行的时间；$$\textit{rest}_i$$表示其剩余执行次数。初始时，所有的 $$\textit{nextValid}_i$$ 均为 $$1$$，而 $$\textit{rest}_i$$即为任务 $$i$$ 在数组 $$\textit{tasks}$$ 中出现的次数。

我们用 $$\textit{time}$$ 记录当前的时间。根据我们的策略，我们需要选择不在冷却中并且剩余执行次数最多的那个任务，也就是说，我们需要找到满足 $$\textit{nextValid}_i \leq \textit{time}$$ 的并且 $$\textit{rest}_i$$ 最大的索引 $$i$$。因此我们只需要遍历所有的二元组，即可找到 $$i$$。在这之后，我们将 $$(\textit{nextValid}_i, \textit{rest}_i)$$ 更新为 $$(\textit{time}+n+1, \textit{rest}_i-1)$$，记录任务 $$i$$ 下一次冷却结束的时间以及剩余执行次数。如果更新后的 $$\textit{rest}_i=0$$，那么任务 $$i$$ 全部做完，我们在遍历二元组时也就可以忽略它了。

而对于 $$\textit{time}$$ 的更新，我们可以选择将其不断增加 $$1$$，模拟每一个时间片。但这会导致我们在 CPU 处于待命状态时，对二元组进行不必要的遍历。为了减少时间复杂度，我们可以在每一次遍历之前，将 $$\textit{time}$$ 更新为所有 $$\textit{nextValid}_i$$中的最小值，直接「跳过」待命状态，保证每一次对二元组的遍历都是有效的。需要注意的是，只有当这个最小值大于 $$\textit{time}$$ 时，才需要这样快速更新。

证明

对于某个时间点 $$t$$，设任务 $$a$$ 和 $$b$$ 均不在冷却中，并且它们分别剩余 $$p$$ 和 $$q$$ 次。不失一般性，假设 $$p>q$$，那么我们应当在此时选择任务 $$a$$，但我们选择了任务 $$b$$。我们需要证明，存在一种交换方法，使得将此时的任务 $$b$$「变成」任务 $$a$$ 后，总时间不会增加。

为了叙述方便，设 $$a_1, a_2, \cdots, a_p$$ 为选择任务 $$a$$ 的时间点，$$b_1, b_2, \cdots, b_q$$ 为选择任务 bb 的时间点，根据假设有
$$
a_1 > b_1 = t
$$
以及对于任意相邻的两项 $$a_i, a_{i+1}$$ 或者 $$b_j, b_{j+1}$$ ，均有
$$
a_{i+1} - a_i > n
$$
以及

$$
b_{j+1} - b_j > n
$$
接下来我们分情况讨论：

  • 如果 $$\exists k’ \in [2, q]$$ ，使得 $$a_{k’} < b_{k’}$$，那么我们找出其中最小的那个 $$k’$$ 记为 $$k$$。此时我们有
    $$
    \begin{cases} a_1 > b_1 \ a_2 > b_2 \ \cdots \ a_{k-1} > b_{k-1} \ a_k < b_k \end{cases}
    $$

那么我们可以构造序列：

  • $$b_1, b_2, \cdots, b_{k-1}, a_k, a_{k+1}, \cdots, a_p$$ 作为交换后选择任务 $$a$$ 的时间点；
  • $$a_1, a_2, \cdots, a_{k-1}, b_k, b_{k+1}, \cdots, b_q$$ 作为交换后选择任务 $$b$$ 的时间点。

对于交换后任务 $$a$$ 的序列，其一共有 $$p$$ 项，并且有

$$
a_k - b_{k-1} > a_k - a_{k-1} > n
$$

因此其满足任意相邻两项之差大于 $$n$$，不会违反冷却时间的规则。

同理对于对于交换后任务 $$b$$ 的序列，其一共有 $$q$$ 项，并且有

$$
b_k - a_{k-1} > a_k - a_{k-1} > n
$$
同样不会违反冷却时间的规则。

  • 如果 $$\forall k’ \in [2, q]$$ 均有 $$a_{k’} > b_{k’}$$ ，那么我们只要构造序列：
    • $$b_1, b_2, \cdots, b_k$$ 作为交换后选择任务 $$a$$ 的时间点；
    • $$a_1, a_2, \cdots, a_k, b_{k+1}, \cdots, b_n$$作为交换后选择任务 $$b$$ 的时间点。

由于 $$b_{k+1} - a_k > b_{k+1} - b_k > n$$，因此不会违反冷却时间的规则。

无论哪一种情况，我们都将 $$b_1=t$$ 变成了选择任务 $$a$$ 的时间点，并且由于我们只在任务 $$a$$ 和 $$b$$ 的内部进行交换，因此交换后总时间一定不会增加。这样就证明了一定存在一种总时间最少的方法，是通过不断地选择不在冷却中并且剩余执行次数最多的那个任务得到的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * @param {character[]} tasks
 * @param {number} n
 * @return {number}
 * 模拟法
 */
var leastInterval = function(tasks, n) {
    const freq = _.countBy(tasks);

    // 任务总数
    const m = Object.keys(freq).length;
    const nextValid = new Array(m).fill(1);
    const rest = Object.values(freq);

    let time = 0;
    for (let i = 0; i < tasks.length; i++) {
        time++;
        let minNextValid = Number.MAX_VALUE;
        for (let j = 0; j < m; j++) {
            if (rest[j] > 0) {
                minNextValid = Math.min(nextValid[j], minNextValid);
            }
        }
        time = Math.max(time, minNextValid);

        let best = -1;
        for (let j = 0; j < m; j++) {
            if (rest[j] && nextValid[j] <= time) {
                if (best === -1 || rest[j] > rest[best]) {
                    best = j;
                }
            }
        }

        nextValid[best] = time + n + 1;
        rest[best]--;
    }

    return time;
};

构造+贪心

我们首先考虑所有任务种类中执行次数最多的那一种，记它为 $$\texttt{A}$$，的执行次数为 $$\textit{maxExec}$$。

我们使用一个宽为 $$n+1$$ 的矩阵可视化地展现执行 $$\texttt{A}$$ 的时间点。其中任务以行优先的顺序执行，没有任务的格子对应 $$CPU$$ 的待命状态。由于冷却时间为 $$n$$，因此我们将所有的 $$\texttt{A}$$ 排布在矩阵的第一列，可以保证满足题目要求，并且容易看出这是可以使得总时间最小的排布方法，对应的总时间为：

$$
(\textit{maxExec} - 1)(n + 1) + 1
$$
同理，如果还有其它也需要执行 $$\textit{maxExec}$$ 次的任务，我们也需要将它们依次排布成列。例如，当还有任务 $$\texttt{B}$$ 和 $$\texttt{C}$$ 时，我们需要将它们排布在矩阵的第二、三列。

img

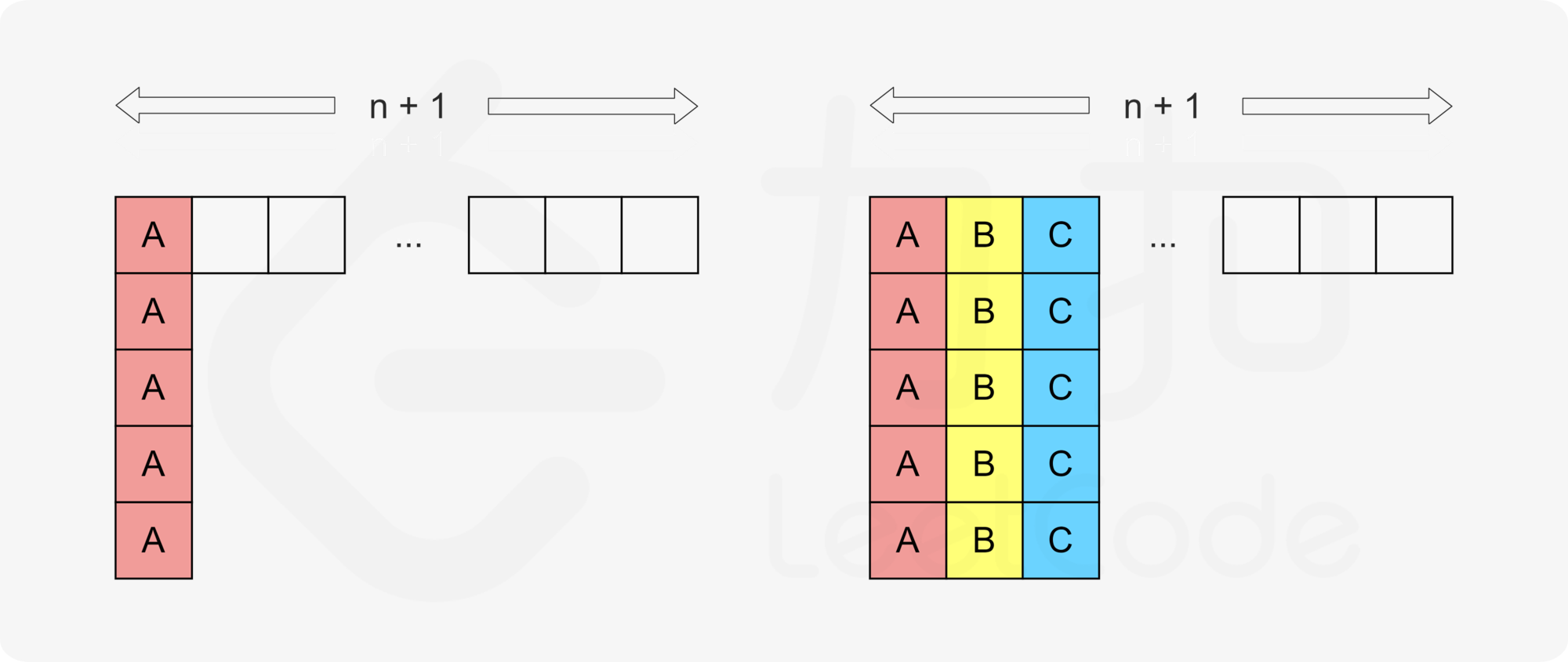
如果需要执行 $$\textit{maxExec}$$ 次的任务的数量为 $$\textit{maxCount}$$，那么类似地可以得到对应的总时间为：

$$
(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$

读者可能会对这个总时间产生疑问：如果 $$\textit{maxCount} > n+1$$，那么多出的任务会无法排布进矩阵的某一列中，上面计算总时间的方法就不对了。我们把这个疑问放在这里，先「假设」一定有 $$\textit{maxCount} \leq n+1$$。

处理完执行次数为 $$\textit{maxExec}$$ 次的任务，剩余任务的执行次数一定都小于 $$\textit{maxExec}$$，那么我们应当如何将它们放入矩阵中呢？一种构造的方法是，我们从倒数第二行开始，按照反向列优先的顺序（即先放入靠左侧的列，同一列中先放入下方的行），依次放入每一种任务，并且同一种任务需要连续地填入。例如还有任务 $$\texttt{D}$$，$$\texttt{E}$$ 和 $$\texttt{F}$$ 时，我们会按照下图的方式依次放入这些任务。

img

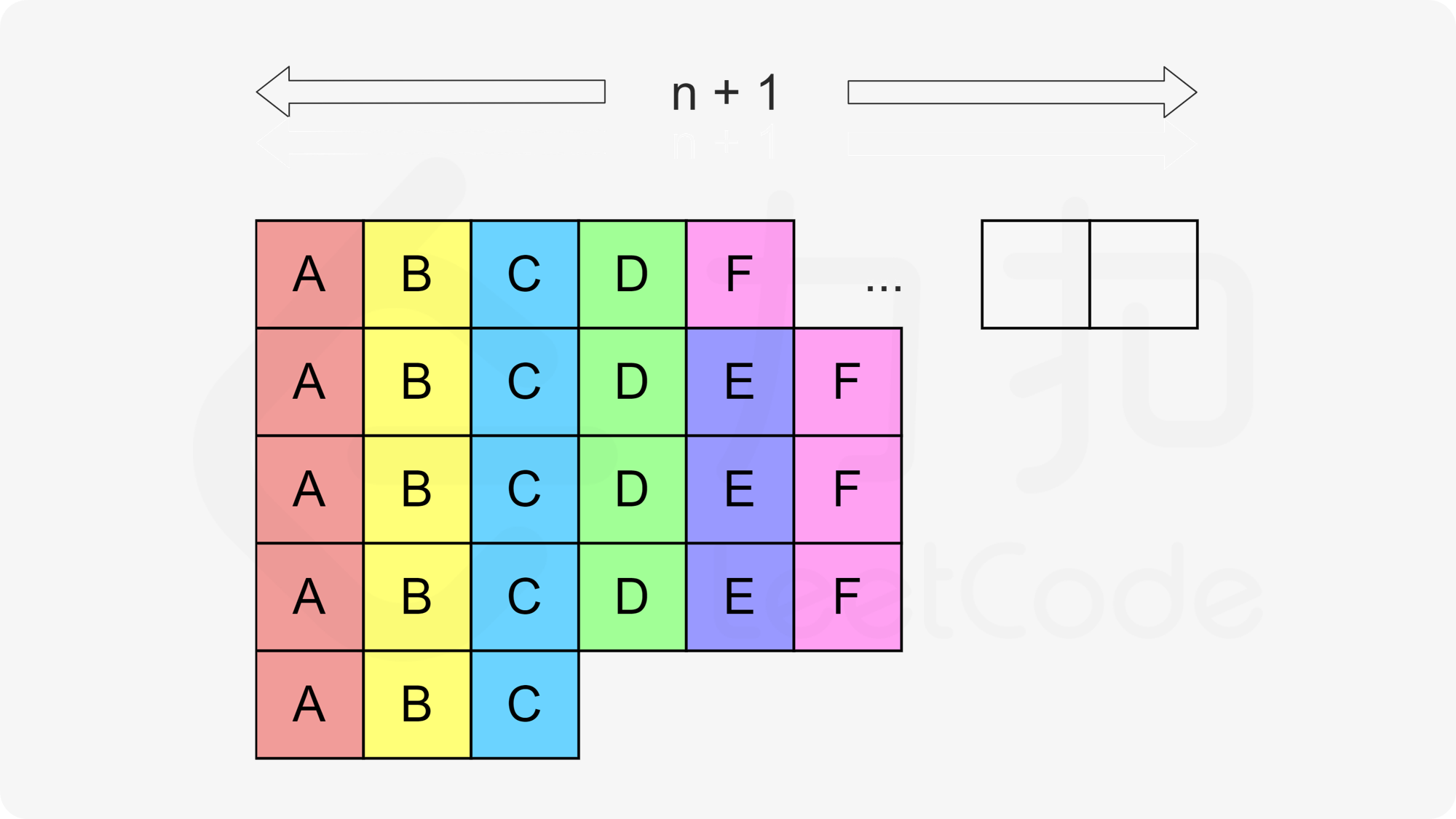
对于任意一种任务而言，一定不会被放入同一行两次（否则说明该任务的执行次数大于等于 $$\textit{maxExec}$$），并且由于我们是按照列优先的顺序放入这些任务，因此任意两个相邻的任务之间要么间隔 $$n$$（例如上图中位于同一列的相同任务），要么间隔 $$n+1$$（例如上图中第一列和第二列的 $$\texttt{F}$$），都是满足题目要求的。因此如果我们按照这样的方法填入所有的任务，那么就可以保证总时间不变，仍然为：

$$
(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$
当然，这些都建立在我们的「假设」之上，即我们不会填「超出」 列。但读者可以想一想，如果我们真的填「超出」了 $$n+1$$ 列，会发生什么呢？

img

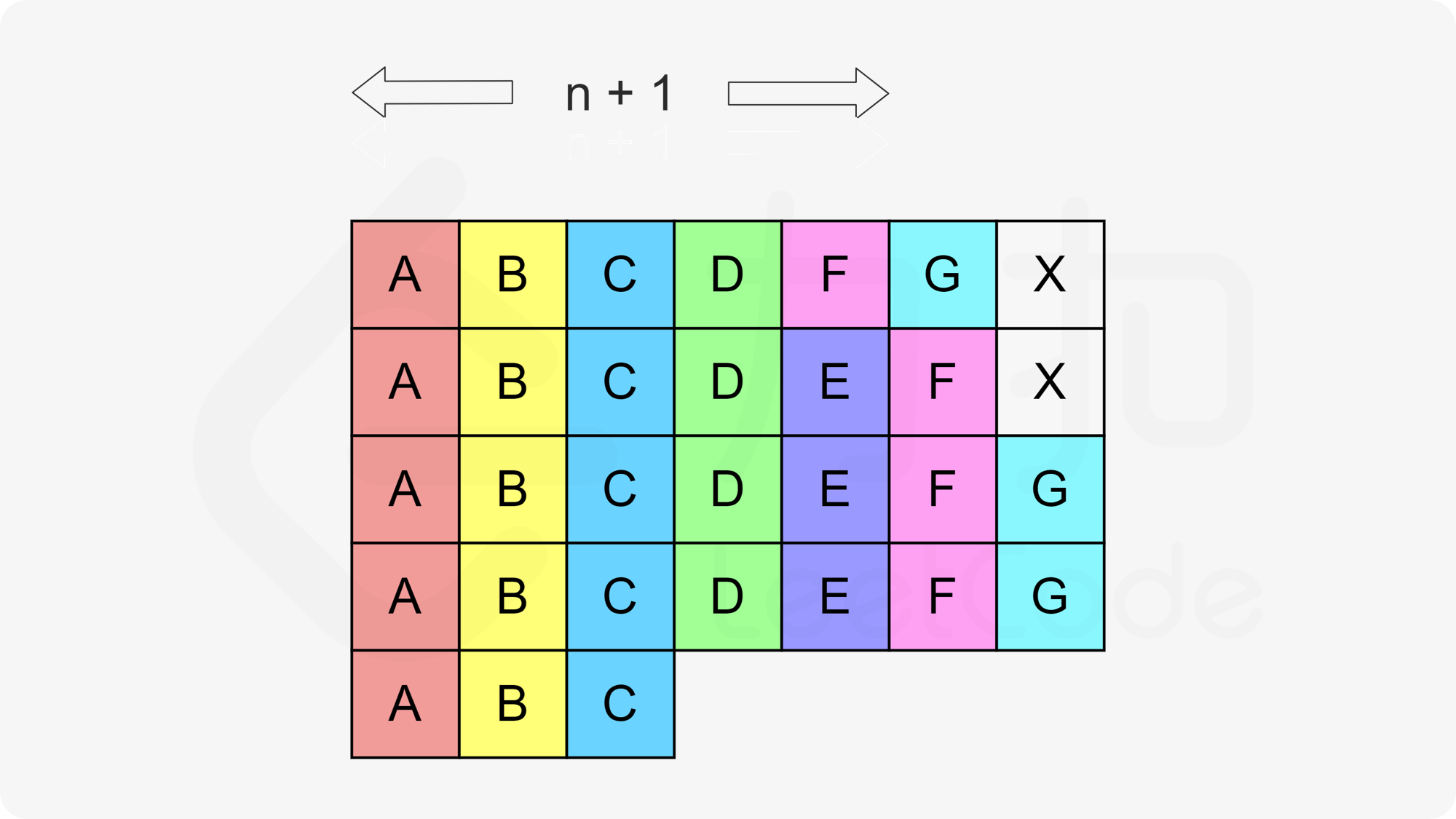
上图给出了一个例子，此时 $$n+1=5$$ 但我们填了 $$7$$ 列。标记为 $$\texttt{X}$$ 的格子表示 CPU 的待命状态。看上去我们需要 $$(5-1) \times 7 + 4 = 32$$ 的时间来执行所有任务，但实际上如果我们填「超出」了 $$n+1$$ 列，那么所有的 CPU 待命状态都是可以省去的。这是因为 CPU 待命状态本身只是为了规定任意两个相邻任务的执行间隔至少为 $$n$$，但如果列数超过了 $$n+1$$，那么就算没有这些待命状态，任意两个相邻任务的执行间隔肯定也会至少为 $$n$$。此时，总执行时间就是任务的总数 $$|\textit{task}|$$。

同时我们可以发现：

如果我们没有填「超出」了 $$n+1$$ 列，那么图中存在 $$0$$ 个或多个位置没有放入任务，由于位置数量为 $$(\textit{maxExec} - 1)(n + 1) + \textit{maxCount}$$，因此有：

$$
|\textit{task}| < (\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$
如果我们填「超出」了 $$n+1$$ 列，那么同理有：

$$
|\textit{task}| > (\textit{maxExec} - 1)(n + 1) + \textit{maxCount}
$$
因此，在任意的情况下，需要的最少时间就是 和 $$|\textit{task}|$$ 中的较大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * @param {character[]} tasks
 * @param {number} n
 * @return {number}
 */
var leastInterval = function(tasks, n) {
    let charsFreq = new Array(26).fill(0);
    let base = 'A'.charCodeAt();
    for (let task of tasks) charsFreq[task.charCodeAt() - base]++;
    charsFreq.sort((a, b)=> b - a);
    let maxOne = charsFreq[0];
    let idx = 0;
    while (idx < 26 && charsFreq[idx] === maxOne) idx++;
    let count = (idx - 0);
    let minTime = Math.max(tasks.length, (maxOne - 1) * (n + 1) + count);
    return minTime;
};

647. 回文子串

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

1
2
3
输入："abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

1
2
3
输入："aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：

  • 输入的字符串长度不会超过 1000 。

中心扩展，尝试着判断是否是回文子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @param {string} s
 * @return {number}
 */
var countSubstrings = function (s) {
    let count = 0;
    for (let i = 0; i < s.length; i++) {
        // 奇数长度
        count += extendSubstrings(s, i, i);
        // 偶数长度
        count += extendSubstrings(s, i, i + 1);
    }
    return count;
}
function extendSubstrings(s, l, r) {
    let count = 0;
    while (l >= 0 && r < s.length && s[l] == s[r]) {
        l--;
        r++;
        count++;
    }
    return count;
}

这个动态规划没什么用啊

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * @param {string} s
 * @return {number}
 */
var countSubstrings = function(s) {
    if (s == null || s.length == 0) {
        return 0;
    }
    let n = s.length;
    let dp = new Array(n);
    let res = n;
    for (let i = 0; i < n; i++) {
        dp[i] = new Array(n);
        dp[i][i] = true;
    }
    // 因为在填dp表时，(i, j) 位置的值依赖于（i+1,j-1），也就是当前位置的左下方。显然如果从上往下遍历，左下方的值就完全没有初始化，当然当前位置也会是错误的。但是从右下角遍历就保证了左下方的所有值都已经计算好了
    for(let i = n - 1; i >= 0; i--){
        for(let j = i+1; j < n; j++){
            if(s[i] == s[j]) {
                if(j - i == 1){
                    dp[i][j] = true;
                }
                else{
                    dp[i][j] = dp[i + 1][j - 1]; 
                }
            } else {
                dp[i][j] = false;
            }
            if(dp[i][j]){
                res++;
            }
        }
    }
    return res;
};

然后马拉车又看不懂了

-------------本文结束感谢您的阅读-------------

欢迎关注我的其它发布渠道