按照算法和数据结构进行分类,一起来刷题,用于自己在面试前查漏补缺。我的意向岗位是前端,选择用javascript来刷题,优点是动态语言,语法简单,缺点是遇见复杂数据结构会出现较难的写法,如堆、并查集,每题对应leetcode的题号。本篇是二叉树
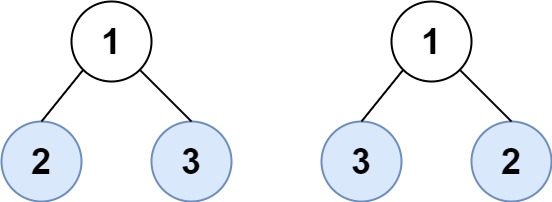
专题部分 二叉树 给定一个二叉树的根节点 root ,返回它的 中序 遍历。
示例 1:
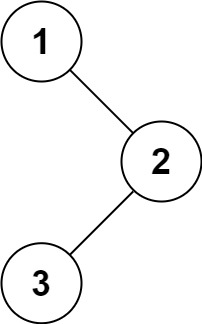
1 2 输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
示例 3:
示例 4:
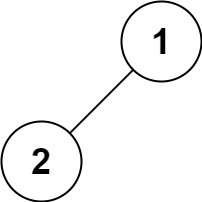
1 2 输入:root = [1,2] 输出:[2,1]
示例 5:
1 2 输入:root = [1,null,2] 输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
递归算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var inorderTraversal = function (root ) let ans = []; let inOrder = function (root ) if (!root) return ; inOrder(root.left); ans.push(root.val); inOrder(root.right); } inOrder(root); return ans; };
迭代法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 var inorderTraversal = function (root ) let res = []; let stack = []; let cur = root; while (stack.length || cur) { while (cur) { stack.push(cur); cur = cur.left; } cur = stack.pop(); res.push(cur.val); cur = cur.right; } return res; };
使用了递归的骚方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 var inorderTraversal = function (root ) if (!root) return []; return inorderTraversal(root.left).concat(root.val, inorderTraversal(root.right)); };
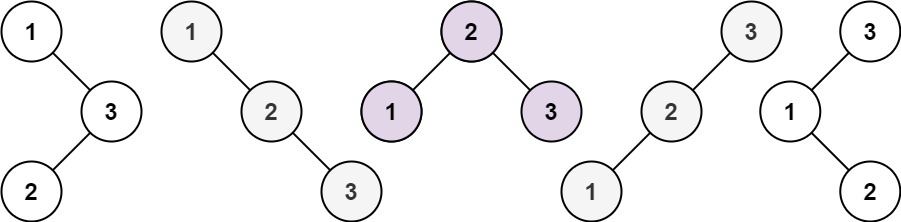
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
示例 2:
提示:
动态规划
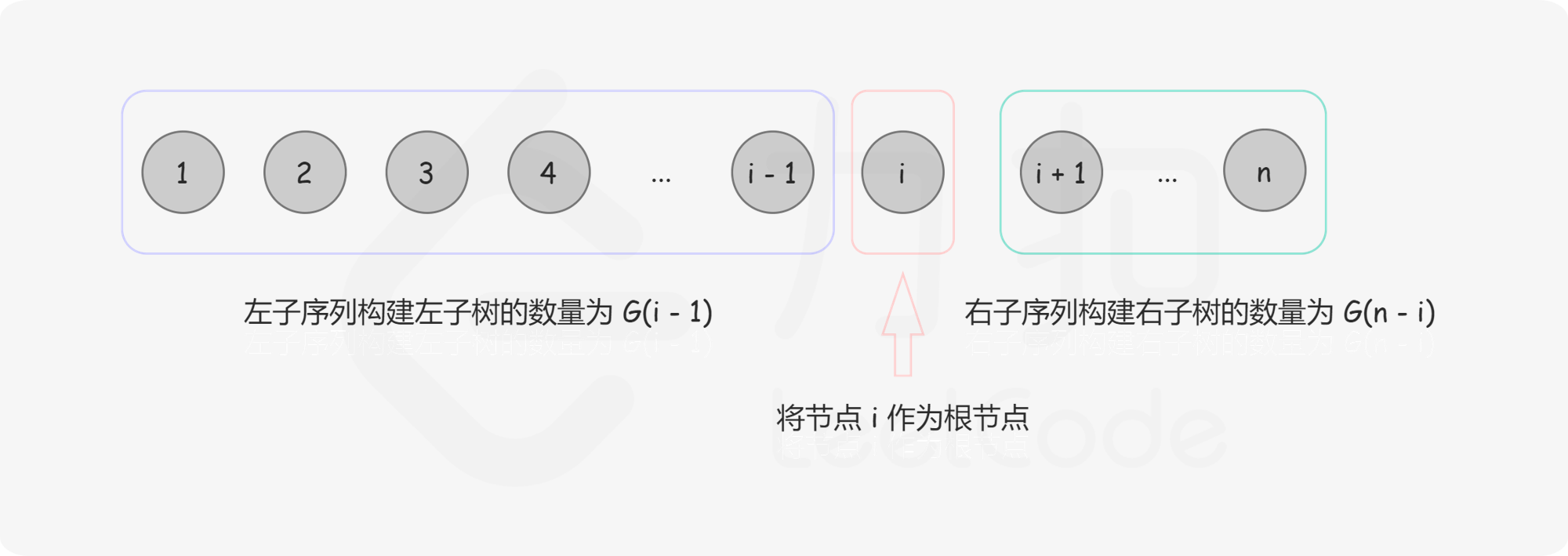
给定一个有序序列 $$1 \cdots n$$,为了构建出一棵二叉搜索树,我们可以遍历每个数字$$i$$,将该数字作为树根,将 $$1 \cdots (i-1)$$ 序列作为左子树,将 $$(i+1) \cdots n$$ 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。
在上述构建的过程中,由于根的值不同,因此我们能保证每棵二叉搜索树是唯一的。
由此可见,原问题可以分解成规模较小的两个子问题,且子问题的解可以复用。因此,我们可以想到使用动态规划来求解本题。
题目要求是计算不同二叉搜索树的个数。为此,我们可以定义两个函数:
$$G(n)$$: 长度为 $$n$$ 的序列能构成的不同二叉搜索树的个数。
$$F(i, n)$$: 以 $$i$$ 为根、序列长度为 $$n$$ 的不同二叉搜索树个数 $$(1 \leq i \leq n)$$。
可见,$$G(n)$$ 是我们求解需要的函数。
稍后我们将看到,$$G(n)$$ 可以从 $$F(i, n)$$ 得到,$$F(i, n)$$ 又会递归地依赖于 $$G(n)$$。
首先,根据上一节中的思路,不同的二叉搜索树的总数 $$G(n)$$,是对遍历所有 $$i (1 \le i \le n)$$的$$F(i, n)$$ 之和。换言之:
$$
$$
举例而言,创建以 3 为根、长度为 7 的不同二叉搜索树,整个序列是 [1, 2, 3, 4, 5, 6, 7],我们需要从左子序列 [1, 2] 构建左子树,从右子序列 [4, 5, 6, 7]构建右子树,然后将它们组合(即笛卡尔积)。
对于这个例子,不同二叉搜索树的个数为 $$F(3, 7)$$。我们将 [1,2] 构建不同左子树的数量表示为 $$G(2)$$, 从 [4, 5, 6, 7] 构建不同右子树的数量表示为 $$G(4)$$,注意到 $$G(n)$$ 和序列的内容无关,只和序列的长度有关。于是,$$F(3,7) = G(2) \cdot G(4)$$。 因此,我们可以得到以下公式:
$$
$$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 var numTrees = function (n ) let G = new Array (n + 1 ).fill(0 ); G[0 ] = 1 , G[1 ] = 1 ; for (let i = 2 ; i <= n; i++) { for (let j = 1 ; j <= i; j++) { G[i] += G[j - 1 ] * G[i - j]; } } return G[n]; };
数学方法
事实上我们在方法一中推导出的 $$G(n)$$函数的值在数学上被称为卡塔兰数 $$C_n$$ 。卡塔兰数更便于计算的定义如下:
$$
1 2 3 4 5 6 7 8 9 10 11 var numTrees = function (n ) let C = 1 ; for (let i = 0 ; i < n; i++) { C = C * 2 * (2 * i + 1 ) / (i + 2 ); } return C; };
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于 当前节点的数。
节点的右子树只包含大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
1 2 3 4 5 输入: 2 / \ 1 3 输出: true
示例 2:
1 2 3 4 5 6 7 8 9 输入: 5 / \ 1 4 / \ 3 6 输出: false 解释: 输入为: [5,1,4,null,null,3,6]。 根节点的值为 5 ,但是其右子节点值为 4 。
如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左右子树也为二叉搜索树。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 let helper = function (node, lower, upper ) if (node == null ) return true ; if (node.val <= lower || node.val >= upper) return false ; return helper(node.left, lower, node.val) && helper(node.right, node.val, upper); } var isValidBST = function (root ) return helper(root, -Infinity , Infinity ); };
中序遍历是从小到大的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 var isValidBST = function (root ) let stack = []; let inorder = -Infinity ; while (stack.length || root !== null ) { while (root !== null ) { stack.push(root); root = root.left; } root = stack.pop(); if (root.val <= inorder) { return false ; } inorder = root.val; root = root.right; } return true ; };
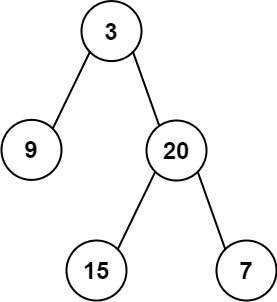
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例: [3,9,20,null,null,15,7],
返回其层序遍历结果:
1 2 3 4 5 [ [3], [9,20], [15,7] ]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 var levelOrder = function (root ) if (root == null ) return []; let queue = [root]; let level = 0 ; let number = []; while (queue.length != 0 ) { let l = queue.length; number[level] = [] for (let i = 0 ; i < l; i++) { let node = queue.shift(); number[level][i] = node.val; if (node.left !== null ) queue.push(node.left); if (node.right !== null ) queue.push(node.right); } level++; } return number; };
给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。
示例 1:
1 2 Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
示例 2:
1 2 Input: preorder = [-1], inorder = [-1] Output: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder 和 inorder 均无重复元素inorder 均出现在 preorderpreorder 保证为二叉树的前序遍历序列inorder 保证为二叉树的中序遍历序列
利用二叉树前序遍历头部是根节点,后面左子树和右子树。中序遍历前面左子树中间根节点最后右子树特点,递归构建
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var buildTree = function (preorder, inorder ) if (preorder.length <= 0 ) return null ; let node = new TreeNode(preorder[0 ]); let i = inorder.indexOf(preorder[0 ]); node.left = buildTree(preorder.slice(1 , i + 1 ), inorder.slice(0 , i)); node.right = buildTree(preorder.slice(i + 1 , preorder.length), inorder.slice(i + 1 , inorder.length)); return node; };
使用哈希存储空间换时间
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 let preorder_qt;let hashMap = {};var buildTree = function (preorder, inorder ) let len = inorder.length; for (let i = 0 ;i<len;i++) { hashMap[inorder[i]] = i; } preorder_qt = preorder; return dg(0 , len); }; let dg = function (in_left,in_right ) if (in_left >= in_right) return null ; let val = preorder_qt.shift(); let root = new TreeNode(val); let index = hashMap[val]; root.left = dg(in_left, index); root.right = dg(index + 1 ,in_right); return root; }
改用迭代法,使用栈实现构建
迭代法是一种非常巧妙的实现方法。
对于前序遍历中的任意两个连续节点 u 和 v,根据前序遍历的流程,我们可以知道 u 和 v 只有两种可能的关系:
v 是 u 的左儿子。这是因为在遍历到 u 之后,下一个遍历的节点就是 u 的左儿子,即 v;
u 没有左儿子,并且 v 是 u 的某个祖先节点(或者 u 本身)的右儿子。如果 u 没有左儿子,那么下一个遍历的节点就是 u 的右儿子。如果 u 没有右儿子,我们就会向上回溯,直到遇到第一个有右儿子(且 u 不在它的右儿子的子树中)的节点 $$u_a$$ ,那么 v 就是 $$u_a$$ 的右儿子。
归纳出算法流程:
最后得到的二叉树即为答案。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 var buildTree = function (preorder, inorder ) if (preorder.length === 0 ) { return null ; } const treeNodeList = []; const root = new TreeNode(preorder[0 ]); treeNodeList.push(root); let j = 0 ; for (let i = 1 ; i < preorder.length; i++) { const current = new TreeNode(preorder[i]); let curParent; while (treeNodeList.length !== 0 && treeNodeList[treeNodeList.length - 1 ].val === inorder[j]) { curParent = treeNodeList[treeNodeList.length - 1 ]; treeNodeList.length--; j++; } if (curParent) { curParent.right = current; } else { treeNodeList[treeNodeList.length - 1 ].left = current; } treeNodeList.push(current); } return root; };
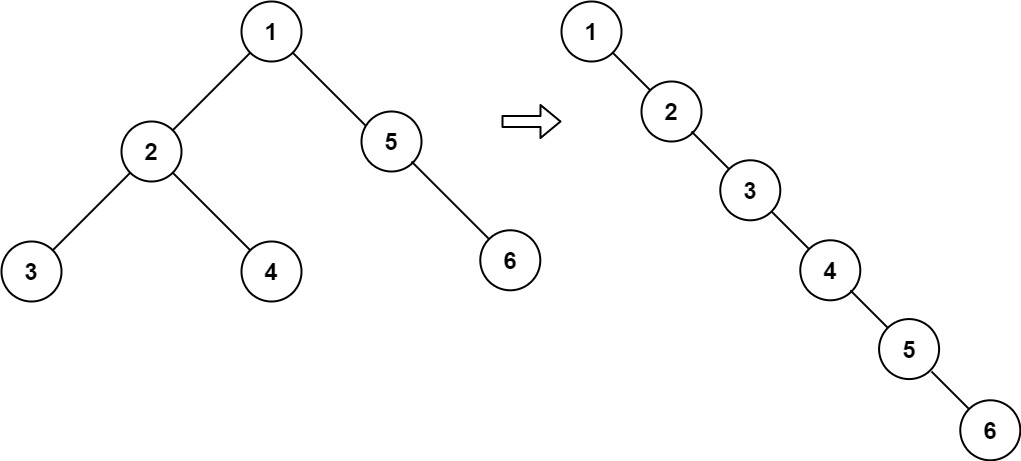
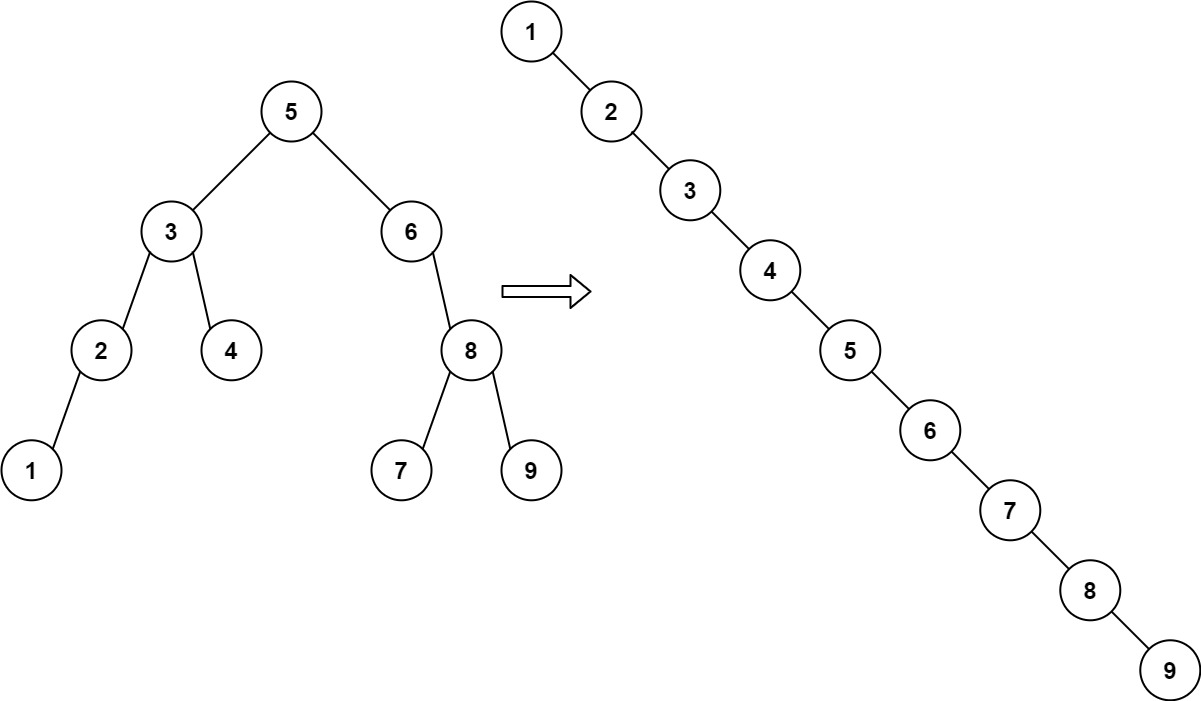
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历
示例 1:
1 2 输入:root = [1,2,5,3,4,null,6] 输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
示例 3:
提示:
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100
进阶: 你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
维护上一个访问的节点 prev,每次访问一个节点时,令当前访问的节点为 curr,将 prev 的左子节点设为 null 以及将 prev 的右子节点设为 curr,然后将 curr 赋值给 prev,进入下一个节点的访问,直到遍历结束。需要注意的是,初始时 prev 为 null,只有在 prev 不为 null 时才能对 prev 的左右子节点进行更新。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 var flatten = function (root ) if (root == null ) return null ; let stack = [], node = null , cur = new TreeNode('head' ); stack.push(root); while (stack.length) { node = stack.pop(); cur.right = node; cur.left = null ; if (node.right){ stack.push(node.right); } if (node.left){ stack.push(node.left); } cur = cur.right; } return root; };
要想做到O(1) 额外空间,不能存储已遍历节点,只能保存上一个指针
注意到前序遍历访问各节点的顺序是根节点、左子树、右子树。如果一个节点的左子节点为空,则该节点不需要进行展开操作。如果一个节点的左子节点不为空,则该节点的左子树中的最后一个节点被访问之后,该节点的右子节点被访问。该节点的左子树中最后一个被访问的节点是左子树中的最右边的节点,也是该节点的前驱节点。因此,问题转化成寻找当前节点的前驱节点。
具体做法是,对于当前节点,如果其左子节点不为空,则在其左子树中找到最右边的节点,作为前驱节点,将当前节点的右子节点赋给前驱节点的右子节点,然后将当前节点的左子节点赋给当前节点的右子节点,并将当前节点的左子节点设为空。对当前节点处理结束后,继续处理链表中的下一个节点,直到所有节点都处理结束。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 var flatten = function (root ) let curr = root; while (curr !== null ) { if (curr.left !== null ) { const next = curr.left; let predecessor = next; while (predecessor.right !== null ) { predecessor = predecessor.right; } predecessor.right = curr.right; curr.left = null ; curr.right = next; } curr = curr.right; } };
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
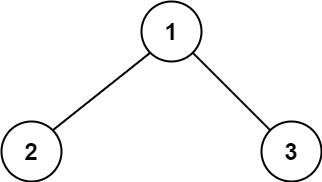
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:
1 2 3 输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
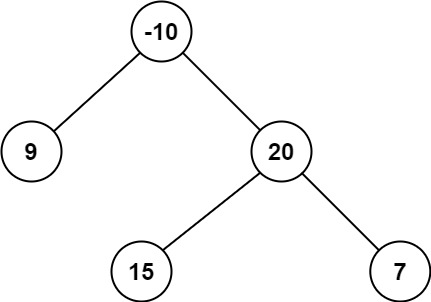
示例 2:
1 2 3 输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
从计算每个节点开始的路径,找到最大路径和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 var maxPathSum = function (root ) let maxSum = Number .MIN_SAFE_INTEGER; function dfs (root ) if (!root) return 0 ; const left = Math .max(0 , dfs(root.left)); const right = Math .max(0 , dfs(root.right)); maxSum = Math .max(maxSum, left + root.val + right); return root.val + Math .max(left, right); } dfs(root); return maxSum; };
翻转一棵二叉树。
示例:
输入:
1 2 3 4 5 4 / \ 2 7 / \ / \ 1 3 6 9
输出:
1 2 3 4 5 4 / \ 7 2 / \ / \ 9 6 3 1
备注: Max Howell 的 原问题 启发的 :
谷歌:我们90%的工程师使用您编写的软件(Homebrew),但是您却无法在面试时在白板上写出翻转二叉树这道题,这太糟糕了。
递归翻转
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 var invertTree = function (root ) if (!root) return null ; let temp = root.left; root.left = root.right; root.right = temp; invertTree(root.left); invertTree(root.right); return root; };
利用栈实现翻转
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var invertTree = function (root ) if (!root) return root; const stack = [root]; while (stack.length) { const node = stack.pop(); [node.left, node.right] = [node.right, node.left]; if (node.left) stack.push(node.left); if (node.right) stack.push(node.right); } return root; };
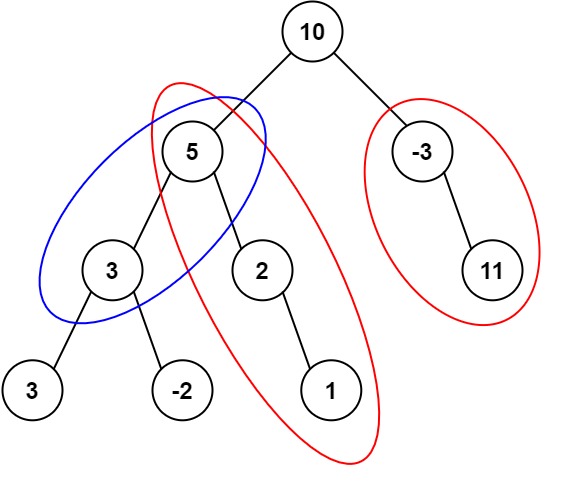
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
示例 1:
1 2 3 输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8 输出:3 解释:和等于 8 的路径有 3 条,如图所示。
示例 2:
1 2 输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22 输出:3
提示:
二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109 -1000 <= targetSum <= 1000
创建一个辅助函数计算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 var pathSum = function (root, sum ) if (root == null ) return 0 ; let pathImLeading = count(root, sum); let leftPathSum = pathSum(root.left, sum); let rightPathSum = pathSum(root.right, sum); return pathImLeading + leftPathSum + rightPathSum; }; function count (node, sum ) if (node == null ) return 0 ; let isMe = (node.val == sum) ? 1 : 0 ; let leftBrother = count(node.left, sum - node.val); let rightBrother = count(node.right, sum - node.val); return isMe + leftBrother + rightBrother; };
简化
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 var pathSum = function (root, sum ) return root ? pathSumStartWithRoot(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum): 0 ; } function pathSumStartWithRoot (root, sum ) if (!root) { return 0 ; } let count = root.val == sum ? 1 : 0 ; count += pathSumStartWithRoot(root.left, sum - root.val); count += pathSumStartWithRoot(root.right, sum - root.val); return count; }
题目描述
给定一棵二叉树,已经其中没有重复值的节点,请判断该二叉树是否为搜索二叉树和完全二叉树。
示例1
输入
返回值
备注:
使用
采用迭代法分别中序遍历和广度优先遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 function judgeIt ( root ) let res = [true , true ]; let pre = -Infinity ; let stack = []; let cur = root; while (stack.length || cur) { while (cur) { stack.push(cur); cur = cur.left; } cur = stack.pop(); if (cur.val < pre) { res[0 ] = false ; break ; } pre = cur.val; cur = cur.right; } let queue = [root]; while (queue[0 ] !== null ) { let node = queue.shift(); queue.push(node.left); queue.push(node.right); } while (queue.length && queue[0 ] === null ) { queue.shift(); } if (queue.length) res[1 ] = false ; return res; } module .exports = { judgeIt : judgeIt };
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
返回 3 , 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意: 两结点之间的路径长度是以它们之间边的数目表示。
DFS遍历,返回节点深度,然后左子树深度+右子树深度+1即为直径
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 var diameterOfBinaryTree = function (root ) if (root === null ) return 0 ; let ans = 0 ; let maxDepth = (root ) => { if (root === null ) return 0 ; let L = maxDepth(root.left); let R = maxDepth(root.right); ans = Math .max(ans, L + R); return Math .max(L, R) + 1 ; } maxDepth(root); return ans; };
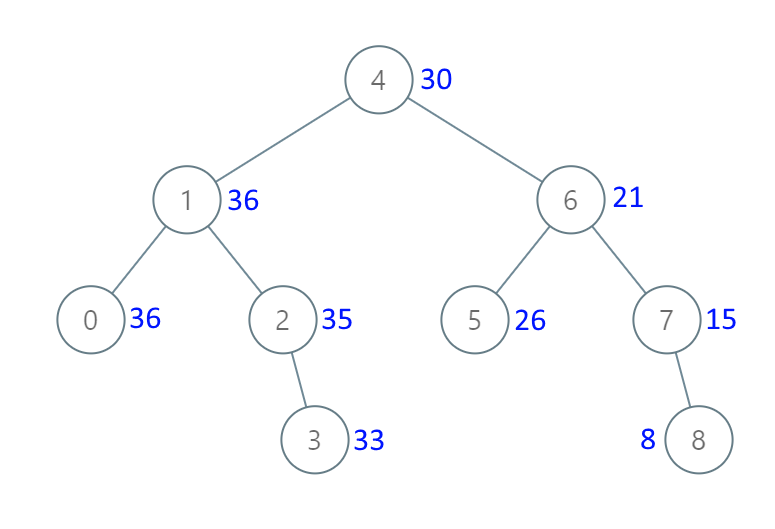
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
注意: 本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:
1 2 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
1 2 输入:root = [0,null,1] 输出:[1,null,1]
示例 3:
1 2 输入:root = [1,0,2] 输出:[3,3,2]
示例 4:
1 2 输入:root = [3,2,4,1] 输出:[7,9,4,10]
提示:
树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。
递归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 var convertBST = function (root ) if (!root) return root; let sum = 0 ; let dfs = function (root ) if (root == null ) return ; dfs(root.right); sum += root.val; root.val = sum; dfs(root.left); } dfs(root); return root; };
迭代法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 var convertBST = function (root ) let sum = 0 ; let stack = []; let cur = root; while (cur || stack.length) { while (cur) { stack.push(cur); cur = cur.right; } cur = stack.pop(); sum += cur.val; cur.val = sum; cur = cur.left; } return root; };
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 输入: Tree 1 Tree 2 1 2 / \ / \ 3 2 1 3 / \ \ 5 4 7 输出: 合并后的树: 3 / \ 4 5 / \ \ 5 4 7
注意: 合并必须从两个树的根节点开始。
需要计算和
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 var mergeTrees = function (t1, t2 ) if (t1 === null && t2 === null ) return null ; num1 = t1 === null ? 0 : t1.val; num2 = t2 === null ? 0 : t2.val; let sum = num1 + num2; let node = new TreeNode(sum); node.left = mergeTrees(t1 && t1.left ? t1.left : null , t2 && t2.left ? t2.left : null ); node.right = mergeTrees(t1 && t1.right ? t1.right : null , t2 && t2.right ? t2.right : null ); return node; };
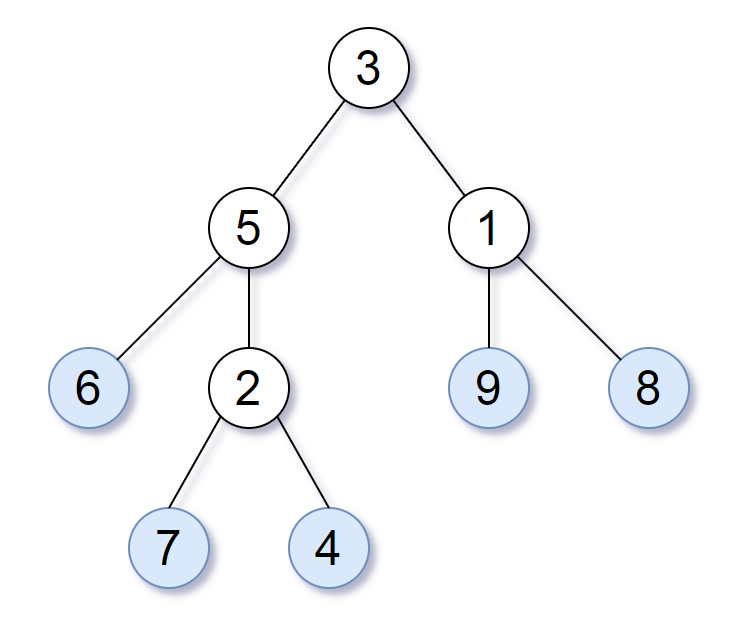
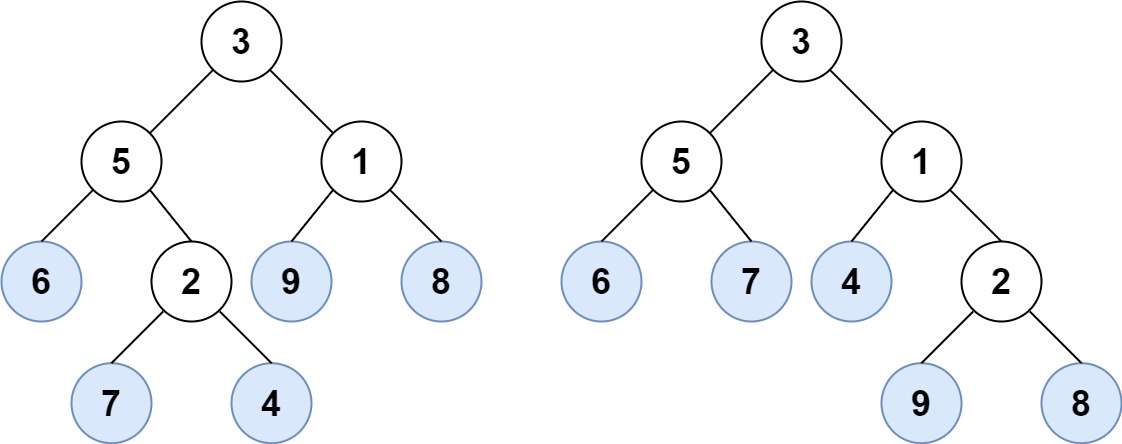
请考虑一棵二叉树上所有的叶子,这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。
举个例子,如上图所示,给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。
如果有两棵二叉树的叶值序列是相同,那么我们就认为它们是 叶相似 的。
如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的,则返回 true;否则返回 false 。
示例 1:
1 2 输入:root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8] 输出:true
示例 2:
1 2 输入:root1 = [1], root2 = [1] 输出:true
示例 3:
1 2 输入:root1 = [1], root2 = [2] 输出:false
示例 4:
1 2 输入:root1 = [1,2], root2 = [2,2] 输出:true
示例 5:
1 2 输入:root1 = [1,2,3], root2 = [1,3,2] 输出:false
提示:
给定的两棵树可能会有 1 到 200 个结点。
可以使用DFS,获取叶子节点的序列,进行比对,我选择了相对麻烦的迭代法,不需要保存叶子节点的序列,但需要用到队列结构占用空间
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 var leafSimilar = function (root1, root2 ) let stack1 = [root1], stack2 = [root2]; while (stack1.length !== 0 && stack2.length !== 0 ) { let node1 = stack1.pop(), node2 = stack2.pop(); while (node1.left || node1.right) { if (node1.left) { if (node1.right) stack1.push(node1.right); node1 = node1.left; } else { node1 = node1.right; } } while (node2.left || node2.right) { if (node2.left) { if (node2.right) stack2.push(node2.right); node2 = node2.left; } else { node2 = node2.right; } } if (node1.val !== node2.val) return false ; } return stack1.length === 0 && stack2.length === 0 ; };
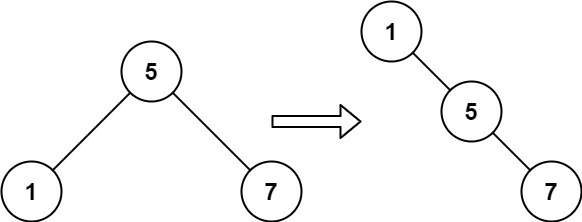
给你一棵二叉搜索树,请你 按中序遍历 将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:
1 2 输入:root = [5,3,6,2,4,null,8,1,null,null,null,7,9] 输出:[1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
示例 2:
1 2 输入:root = [5,1,7] 输出:[1,null,5,null,7]
提示:
树中节点数的取值范围是 [1, 100]
0 <= Node.val <= 1000
采用中序遍历深度优先遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 var increasingBST = function (root ) let pre, head; function inOrderTravel (node ) if (!node) {return ; } inOrderTravel(node.left); if (pre) { pre.right = node; node.left = null ; pre = node; } else { head = node; pre = node; } inOrderTravel(node.right); } inOrderTravel(root); return head; };
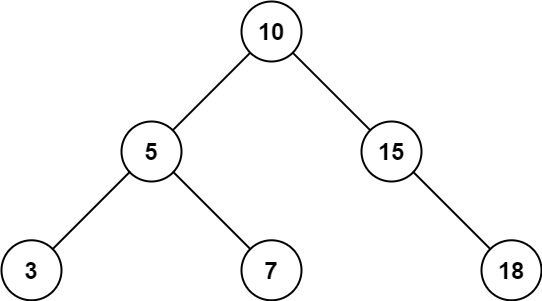
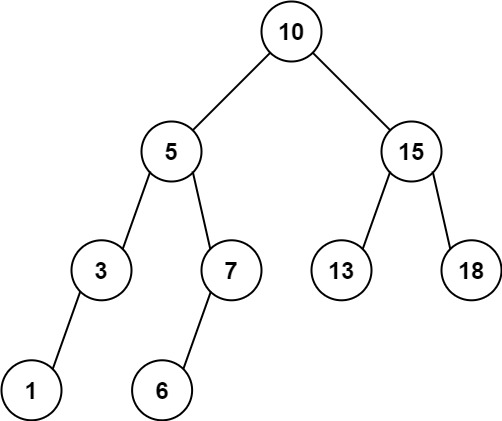
给定二叉搜索树的根结点 root,返回值位于范围 [low, high]
示例 1:
1 2 输入:root = [10,5,15,3,7,null,18], low = 7, high = 15 输出:32
示例 2:
1 2 输入:root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 输出:23
提示:
树中节点数目在范围 [1, 2 * 104] 内
1 <= Node.val <= 105
1 <= low <= high <= 105
所有 Node.val 互不相同
按深度优先搜索的顺序计算范围和。记当前子树根节点为 \textit{root}root,分以下四种情况讨论:
root 节点为空
返回 0。
root 节点的值大于high
由于二叉搜索树右子树上所有节点的值均大于根节点的值,即均大于 high,故无需考虑右子树,返回左子树的范围和。
root 节点的值小于low
由于二叉搜索树左子树上所有节点的值均小于根节点的值,即均小于 low,故无需考虑左子树,返回右子树的范围和。
root 节点的值在 [low,high] 范围内
此时应返回 root 节点的值、左子树的范围和、右子树的范围和这三者之和。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 var rangeSumBST = function (root, L, R ) if (!root) return 0 ; if (root.val < L) return rangeSumBST(root.right, L, R); if (root.val > R) return rangeSumBST(root.left, L, R); return root.val + rangeSumBST(root.left, L, R) + rangeSumBST(root.right, L, R); };